Como esse é um tópico grande, este post abordará o básico sobre como reconhecer os diferentes tipos de complexidade do Big O, como O(n), O(2n), O(n²), O(log n), etc.
Complexidade de tempo e espaço
A notação Big O pode ser utilizada para descrever a complexidade de uma seção de código em termos de tempo de execução e espaço. Assim, a complexidade do tempo do Big O descreve o tempo de execução no pior e no melhor cenário.
Já a complexidade Big O relativa ao espaço, descreve quanta memória é necessária para executar uma seção de código no pior cenário. Por exemplo, um loop em uma instrução for que copia uma matriz precisará de muito mais memória para ser executado do que se esse memo loop simplesmente modificar uma matriz existente.
Vejamos duas funções para ver como a noação Big O descreve os tempos de execução.
A função acima acessa e atribui apenas um valor em um local, o tempo de execução será o mesmo, se o comprimento da matriz for de 10 unidades ou 10 milhões. Se o tempo de execução for constante, independentemente da entrada, diz-se que a função possui uma complexidade de tempo de O(1).
Quanto ao espaço, como a matriz já existe na memória e a função está apenas atualizando os valores na matriz, a função não uytiliza memória adicional, independentemente do tamanho da matriz. Isso significa que a função também tem uma complexidade espacial de O(1).
Agora vamos avaliar um outro exemplo:
Na função double_and_copy_list_values, o valor em cada índice da matriz é dobrado a cada iteração. Ou seja, há um aumento linear de iterações no loop à medida que o comprimento da matriz aumenta, diz-se então que esse código tem uma complexidade de tempo de execução de \(O(n)\). Além disso, a instrução agora utiliza memória adicional, que por sua vez aumenta linearmente à medida que o comprimento da matriz aumenta. Isso significa que a função tem uma complexidade de espaço de O(n).
Dados esses dois exemplos, fica claro que o primeiro trecho de código, com uma complexidade de tempo de O(1) será executado mais rapidamente em quase todos os casos.
É possível encontrar uma entrada específica em que uma função \(O(n)\) performe mais rapidamente do que a função \(O(1)\) ?
Claro, mas geralmente à medida que a complexidade de uma função aumenta, o tempo de execução do pior cenário também aumenta.
A função de crescimento
Uma pergunta que você pode estar se fazendo nesse momento é: Como é possível categorizar um algoritmo complexo usando uma notação tão simples como a Big O?.
“Utilizando a função de crescimento”.
Todo algoritmo é codificado para resolver problemas. Tomando como base uma situação hipotética, considere um algoritmo utilizado para classificar uma matriz e definir sua análise de eficiência. Precisamos saber quão bem esse algoritmo pode executar e para isso é necessário conhecer 2 fatores:
- O tamanho do problema: ou seja, o tamanho da matriz.
- O processo principal que influenciará o tempo do resultado: Aqui estão incluídos o número de comparações que precisaríamos fazer (quanto mais comparações, mais lento será o algoritmo).
Ou seja, a eficiência do algoritmo pode ser definida em termos do tamanho do problema e processamento. Uma função de crescimento mostra o relacionamento entre esses dois fatores, trazendo à tona a complexidade de tempo e/ou espaço em relação ao tamanho do problema.
Antes de iniciar a próxima seção, vamos assumir uma função de crescimento aleatoria, para um algoritmo qualquer de classificação seja expresso pela seguinte notação:
\begin{align} f(n) = 2n^2 + 4n + 6 \end{align}
A complexidade assintótica
Não podemos medir todas as complexidades algoritimcas simplesmente relacionando tempo e espaço arbitráriamente, portanto, em vez de conhecer a eficiência exata, precisamos conhecer a “complexidade assintótica” definida pelo termo dominante de uma função de crescimento.
Na complexidade assintótica, um termo dominante é um termo que aumenta mais rapidamente à medida que o tamanho do problema aumenta.
Segundo [1], Quando observamos tamanhos de entrada grandes o suficiente para tornar relevante apenas a ordem de crescimento do tempo de execução, estamos estudando a eficiência assintótica dos algoritmos. Ou seja, estamos preocupados com a forma como o tempo de execução de um algoritmo aumenta com o tamanho da entrada no limite, à medida que o tamanho da entrada aumenta sem limite. Normalmente, um algoritmo assintoticamente mais eficiente será a melhor opção para todas as entradas, exceto as muito pequenas.
Para a função de crescimento que definimos anteriormente, vamos desenhar uma tabela:
| \(n\) | \(2n^2\) | \(4n\) | \(6\) | \(f(n)\) |
|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 12 |
| 10 | 200 | 40 | 6 | 246 |
| 15 | 450 | 60 | 6 | 516 |
| 20 | 800 | 80 | 6 | 886 |
| 25 | 1250 | 100 | 6 | 1356 |
| 30 | 1800 | 120 | 6 | 1926 |
| 35 | 2450 | 140 | 6 | 2596 |
| 40 | 3200 | 160 | 6 | 3366 |
Considerando nossa função aleatória \(f(n)=2n²+4n+6\), é possível observar que, à medida que n cresce, o termo \(2n^2\) domina o resultado da função, que é \(f(n)\). Portanto, neste caso, \(2n^2\) é o nosso termo dominante.
Apenas um disclaimer antes de prosseguir:
Dizer que um termo é dominante à medida que \(n\) cresce, NÂO significa que ele seja maior que os outros termos para todos os valores de \(n\). Observe que quando \(n = 1\), os termos \(4n\) e a constante \((6)\) são maiores que \(2n^n\). Baseando-se nas considerações acima, podemos, de forma grosseira, definir a seguinte equação:
\begin{align} Big \ O = Complexidade \ Assintótica = Termo \ Dominante \end{align}
Podemos então dizer que a complexidade assintótica da fórmula acima é \(O(2n^2)\) ?
De fato, sim, mas a complexidade assintótica também é chamada de “ordem do algoritmo”. Vamos assumir que a palavra “ordem” aqui significa “aproximadamente” e todas as funções de uma mesma ordem são equivalentes. Além disso, como só temos interesse no termo dominante, isso significa que podemos ignorar outros termos e constantes.
Eliminando a constante \(2\) chegamos a conclusão que a função acima pertence então à ordem \(n^2\). Então, finalmente conseguimos ver algo familiar: \(O(n^2)\)
Defnidos alguns dos conceitos que sustentam a notação Big O, vamos ver alguns exemplos e regras que você pode aplicar ao analisar as notações.
Notação Big O
Como já dito, a notação Big O é uma maneira de medir a eficiência de algoritmos com base no tempo e no espaço. Para medir a complexidade do tempo, o tamanho da entrada é comparado ao tempo necessário para a execução do algoritmo. O melhor tipo de algoritmo, por exemplo, é aquele que sempre leva a mesma quantidade de tempo para executar, independente do tamanho da entrada.
Para medir a complexidade do espaço, ele compara o tamanho da entrada com a quantidade de memória que um algoritmo usa. Assim, cada algoritmo recebe uma complexidade de tempo, do pior ao melhor caso, sendo a complexidade geral do tempo o caso esperado.
Conhecer as complexidades do tempo nos permite criar algoritmos melhores.
Vamos considerar uma instrução for. É possível executá-lo em uma matriz de 10 itens e ele será executado rapidamente, mas caso a mesma iteração seja executada em uma matriz de 10.000 itens, o tempo de execução será muito mais lento.
O termo \(n\) representa o número de entradas. Logo, anotação Big O permite determinar quanto tempo um algoritmo levará para ser executado em virtude da sua entrada (\(n\)). Isso nos permite entender como um pedaço de código será dimensionado além de medir a eficiência algorítmica.
\(O(1)\)
Considere o trecho de código abaixo:
Essa notação, possui um tempo constante, ou seja, o tempo é consistente para cada execução.
Exemplo: Imagine que você leva exatamente 15 segundos para encher uma xícara de café e, em seguida, essa tarefa específica é considerada concluída. Não importa se você enche uma xícara, ou cem xícaras, você enche cada xícara em um período consistente de tempo.,
Portanto, conforme nosso exemplo acima, não nos preocupamos com \(O(1)\), \(O(2)\), etc. Arredondamos para \(O(1)\), ou seja, nossa operação é uma linha plana em termos de escalabilidade. Independente da entrada essa operação levará a mesma quantidade de tempo.
\(O(n)\)
Agora considere o seguinte código:
Nosso exemplo de loop é \(O(n)\), pois é executado para todos os valores em nossa entrada. As operações aumentam de maneira linear de acordo com as entradas ao longo de uma única iteração para cada item. Assim, o algoritmo é executado em tempo linear.
\(O(n^2)\)
Digamos que desejássemos registrar uma série de pares a partir de uma matriz de itens. Podemos fazer assim:
Uma regra geral é que, se você encontrar loops aninhados, use a multiplicação para calcular a notação. Portanto, em nosso exemplo acima, estamos fazendo \(O(n*n)\) que se torna \(O(n^2)\). Isso é conhecido como tempo quadrático, o que significa que toda vez que o número de elementos aumenta, aumentamos as operações quadraticamente. Normalmente evita-se o código que é executado em \(O(n^2)\), pois o número de operações aumenta significativamente quando você introduz mais elementos. Essa notação também é conhecida como notação de tempo polinomial.
Tempo polinomial é uma função polinomial da entrada. Uma função polinomial parece \(n^2\) ou \(n^3\) e assim por diante.
O algoritmo de ordenação Bubblesort é um bom exemplo de algoritmo \(O(n^2)\). O algoritmo identifica o primeiro número e o troca pelo número adjacente, se eles estiverem na ordem errada. Faz isso para cada número, até que todos os números estejam na ordem correta — e portanto, classificados.
\(O \ log(n)\)
Um algoritmo logarítmico reduz pela metade uma lista toda vez que é executado. Vamos olhar para a pesquisa binária. Dada a lista ordenada abaixo:
Em linhas gerais o algoritmo segue os seguintes passos:
- Vá para o meio da lista.
- Verifique se esse elemento é a resposta.
- Caso contrário, verifique se esse elemento é mais do que o item que queremos encontrar.
- Se estiver, ignore o lado direito (todos os números acima do ponto médio) da lista e escolha um novo ponto médio.
- Comece novamente, localizando o ponto médio na nova lista.
O algoritmo reduz pela metade a entrada toda vez que itera. Portanto, é logarítmico. Outros exemplos de algoritmos logarítmicos incluem:
\(O(2^n)\)
O tempo exponencial é \(2^n\), em que \(2\) depende das permutações envolvidas.
Esse algoritmo é o mais lento de todos. Assim, digamos que tenhamos uma senha composta apenas por números (10 números, de 0 a 9). queremos quebrar uma senha que tenha um comprimento de n. Com um algorítmo de força bruta em todas as combinações, teremos \(10^n\) combinações possíveis.
Um exemplo de tempo exponencial é encontrar todos os subconjuntos de um conjunto ou testar combinações de hiperparametros para um modelo de Machine Learning.
A notação exponencial cresce dependendo do tamanho da entrada. Os algoritmos exponenciais são os mais custosos, mas, como os algoritmos polinomiais, é possível utilizar um truque ou outro. Digamos que temos que calcular \(10^4\). Seria necessário fazer o seguinte:
\begin{align} 10 ∗ 10 ∗ 10 ∗ 10 = 10^2 * 10^2 \end{align}
Assim, teríamos que calcular \(10^2\) duas vezes!
E se armazenarmos esse valor em algum lugar e o usarmos mais tarde, para não precisarmos recalcular?
Este é o princípio da programação dinâmica.
Quando nos deparamos com um algoritmo exponencial, a programação dinâmica geralmente pode ser usada para otimiza-lo.
Classificação
Agora que entedemos como analisar, conseguimos definir qual o algoritmo mais rápido. Podemos classifica-los do mais rápido ao mais lento na seguinte ordem:
\begin{align} O(1) < O(log \ n) < O(\sqrt{n}) < O(n) < O(n \ log \ n) < O(n^2) < O(n^3) < O(2^n) < O(n!) \end{align}
Aqui está nosso gráfico de notação Big O, onde os números são reduzidos para que possamos ver todas as linhas diferentes e possa entender as enormes diferenças entre essas complexidades.
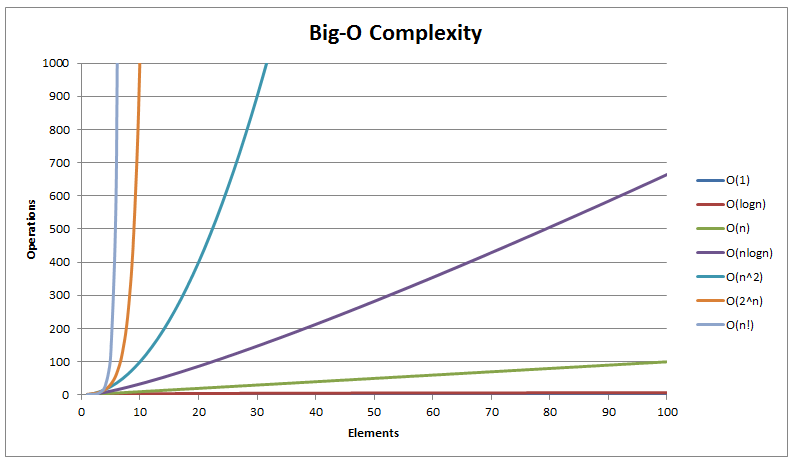
Outras complexidades comuns
Cúbica \(O(n^3)\): — Essa complexidade ocorre normalmente quando executamos 3 loops aninhados, cada \(n\) vezes.
Fatorial \(O(n!)\): — Quando um algoritmo calcula toda a permutação de uma determinada matriz é \(O(n!)\). Um exemplo seria resolver o problema do Caxeiro Viajante por meio da pesquisa de força bruta.
Linearitmica \(O(n \ log \ n)\): — Quando um algoritmo executa operações logarítmicas \(n\) vezes, dizemos que ele tem uma complexidade linearitmica ou \(O(n \ log \ n)\). Um exemplo popular de complexidade linearitmica é o algoritmo Merge sort.
Conclusão
Depois de saber o que realmente está por trás da notação Big O podemos agora definir algumas regras mais gerais que podemos aplicar ao analisar.
-
Remova as constantes. Como já dito no começo desse artigo, se tivermos um algoritmo expresso na forma \(O(2n)\), é possível remover a constante 2 e considerar a complexidade como \(O(n)\).
-
Remova os termos não dominantes. \(O(n^2+n)\) torna-se \(O(n^2)\). Mantenha apenas o termo dominante na notação Big O.
-
Instruções de atribuição são instruções que são executadas apenas uma vez, independentemente do tamanho do problema, são \(O(1)\).
-
Um simples loop
forde 0 a n (sem loops internos) normalmente é \(O(n)\) (complexidade linear); -
Um loop aninhado do mesmo tipo (ou delimitado pelo primeiro parâmetro do loop) fornece \(O(n^2)\) (complexidade quadrática);
-
Um loop no qual o parâmetro de controle é dividido por dois em cada etapa (e que termina quando atinge 1), fornece \(O(log n)\) (complexidade logarítmica);
-
Um loop com instrução
whilepode variar depende do número real de iterações que ele executará. -
Um loop com uma execução não-\(O(1)\) dentro, simplesmente multiplica a complexidade do corpo do loop, pelo número de vezes que o loop será executado.
Uma observação aqui é que, algumas trechos de código podem incluir inicializações e alguns deles podem ser complexos o suficiente para levar em consideração a eficiência de um algoritmo.
É isso?
Sim! A parte mais complicada é descobrir qual é a complexidade do nosso algoritmo incialmente. Simplificar é a parte mais fácil.Para todo caso, lembre-se da regra de ouro da notação Big O e se questione:
“Qual é o pior cenário aqui?”
Caso você queira se aprofundar deixei todo o código utilizado nesse post disponível aqui,
Finalmente, espero que esse material tenha sido útil e faça sentido pra você, principalmente aos iniciantes. Além disso nas referências do artigo é possível encontrar um material muito útil utilizado para elaboração desse artigo que pode te ajudar a ampliar seus conhecimentos no tema.
Lembrando que qualquer feedback, seja positivo ou negativo é so entrar em contato através do meu twitter, linkedin ou nos comentário aqui em baixo. Obrigado :)