O que é Computabilidade?
O termo “computável” foi proposto por Alan Turing para designar a totalidade de números reais cuja expansão decimal pode ser calculada em tempo finito, através de recursos finitos. No mesmo artigo, Turing argumenta que este conjunto corresponde ao conjunto de funções ou predicados computáveis. A proposta de Turing consistia em identificar os possíveis processos envolvidos no ato de “computar um número”. Para tanto, Turing definiu um artefato teórico, que chamou de “máquina de computar”, de maneira que, todo número cuja expansão decimal pudesse ser obtida a partir de operações da máquina seria chamado de “número computado pela máquina” [2].
Fundamentação da Matemática e Paradoxos
Ao final do século XIX os matemáticos se depararam com situações que apontavam a necessidade de uma fundamentação mais cuidadosa da Matemática. Uma destas questões diz respeito ao conceito de séries numéricas, e pode ser ilustrada pelo paradoxo de Zenon:
Aquiles e a Tartaruga decidem apostar uma corrida de 100 metros. Aquiles corre 10 vezes mais rápido do que a tartaruga, e por isto, a tartaruga inicia com 80 metros de vantagem. Aquiles percorre rapidamente a distância inicial que o separa da tartaruga, mas ao alcançar os 80 metros iniciais, a tartaruga já se encontrará 8 metros à frente. Ao alcançar mais 8 metros à frente, a tartaruga já terá avançado mais 0,8 metros, e assim, Aquiles nunca alcançará a tartaruga.
Esse paradoxo tenta provar a impossibilidade do movimento se assumimos que tempo e espaço são infinitamente subdivisíveis [4]. Porém, não podemos esquecer que esse argumento é um argumento abstrato e puramente lógico, logo, sua conclusãoa acaba sendo absurda
O fato é que raciocinando desta forma, os matemáticos do século XIX supunham que a soma de infinitos intervalos é infinita. No entanto a experimentação mostrava que Aquiles alcançaria a tartaruga em pouco tempo. O confronto da observação dos fatos com a explicação matemática demonstrava que o aparato matemático da época era insuficiente para formalizar alguns fenômenos. A solução clássica para esse paradoxo envolve a utilização do conceito de limite e convergência de séries numéricas:os intervalos formam uma progressão geométrica e sua soma converge para um valor finito.
As inquietações dos matemáticos com relação a conceitos não completamente compreendidos e formalizados levaram a grandes avanços neste período. A empolgação com os avanços matemáticos, e particularmente experiências bem sucedidas de explicar conceitos matemáticos através de outros conceitos mais simples conduziram alguns matemáticos a uma abordagem, que, mais tarde ficou conhecida como Abordagem Formalista. Em linhas gerais, os formalistas concebiam a matemática como sistema puramente formal, consistindo na manipulação de símbolos desprovidos de significado ou interpretação[3].
Empenhados em explicar a matemática através de símbolos, regras precisas, e mecanismos finitários, os formalistas se depararam com a descoberta de paradoxos que demonstravam o perigo da matemática “ingênua”, baseada unicamente na intuição. Um destes paradoxos é o paradoxo de Bertrand Russell em 1901, que demonstrou a existência de contradição no interior da teoria (ingênua) dos conjuntos. Apresentamos, a seguir, em sua versão informal:
O barbeiro de Sevilha faz a barba de todas as (e somente das) pessoas em Sevilha que não fazem a barba a si próprias. Pergunta-se: o barbeiro de Sevilha barbeia-se a si próprio?
O paradoxo do barbeiro, semelhante na formulação ao de Russell, foi utilizado por Kurt Gödel para provar o seu teorema da incompletude. Alan Turing provou a indecidibilidade do problema da parada usando o mesmo paradoxo.
Os Problemas de Hilbert
A presença de problemas supostamente verdadeiros ou supostamente falsos permeando todo aparato matemático representava uma ameaça ao rigor matemático que se buscava na época. Matemáticos e filosofos se sentiam incomodados devido a existência de problemas cuja falsidade ou veracidade, até então, não haviam sido provadas.
Assim, Em 1900, o matemático alemão David Hilbert apresentou uma palestra no Segundo Congresso Internacional de Matemática em Paris. Na sua apresentação ele identificou 23 problemas matemáticos e colocou-os como um desafio para o seculo seguinte. Este episódio é peça relevante na busca pela fundamentação da matemática.
Dentre os problemas de Hilbert dois meracem destaque:
Segundo Problema de Hilbert - A não contradição dos axiomas da Aritmética
Na matemática, o segundo problema de Hilbert foi proposto por David Hilbert em 1900, sendo esse um dos seus 23 problemas. Esse problema consiste em provar que a aritmética é consistente - livre de qualquer contradição interna.
Hilbert contrapunha à matemática ideal o conjunto de números naturais e suas manipulações finitárias, ao qual denominava matemática real, e acreditava na matemática como um sistema formal, sustentado por uma pequena quantidade de axiomas, e completo: qualquer proposição expressa naquele sistema poderia ser provada no próprio sistema[3].
Já em 1928 o Programa de Hilbert propunha a formalização da matemática visando garantir rigidez e solidez a toda construção matemática. Em termos gerais, a proposta era reduzir toda matemática a manipulações reais e responder afirmativamente às seguintes questões. A matemática é completa? É consistente? É decidível? E de 1900 a 1929, grande parte da comunidade matemática mundial acreditou na existência de uma matemática segura, finitária, provadamente correta e livre de imprecisões.
Décimo Problema de Hilbert - A decisão sobre a resolubilidade de uma equação diofantina
O décimo problema de Hilbert era conceber um algoritmo que testasse se um polinômio tinha uma raiz inteira. Ele não usou o termo algoritmo, mas sim “um processo com o qual a raiz inteira de um polinômio possa ser determinada por um número finito de operações”. Porém naquela época a inexistencia de um algoritmo para tal tarefa tornava a mesma algoritmicamente insolúvel. Para os matemáticos daquela época chegarem a essa conclusão, com seu conceito ituitivo de algoritmo, teria sido virtualmente impossível. A intuição de algoritmo pode ate ter sido adequada para prover algoritmos para certas tarefas, mas era inútil para mostrar que nenhum algoritmo existe para uma tarefa específica. Provar que um algoritmo não existe requer posse de uma definição clara de algoritmo.
A definição veio nos de 1936 de Alonzo Church e Alan Turing. Church utlizou um sistema notacional denominado \(\lambda\)-cálculo para definir algoritmos. Turing o fez com suas “máquinas”. Essas definições foram demonstradas equivalentes e essa conexão entre a noção informal de algoritmo e a definição precisa veio a ser chamada de tese de Chrurch-Turing
Teoremas da incompletude de Gödel
Em 1930, Kurt Gödel e Gerhard Gentzen provaram resultados que voltaram a chamar atenção para o segundo problema de Hilbert. Alguns autores acreditam que esses resultados resolveram o problema, enquanto outros acreditam que ele ainda está em aberto. Os teoremas, provados por Kurt Gödel em 1931, são importantes tanto para a lógica matemática quanto para a filosofia da matemática. Os dois resultados são amplamente, mas não universalmente, interpretados como indicações de que o programa de Hilbert para encontrar um conjunto completo e consistente de axiomas para toda a matemática é impossível, dando uma resposta negativa para o segundo problema de Hilbert.
O primeiro teorema da incompletude afirma que nenhum sistema consistente de axiomas, cujos teoremas podem ser listados por um “procedimento efetivo” – por exemplo um programa de computador que pode ser qualquer tipo de algoritmo – é capaz de provar todas as verdades sobre as relações dos números naturais (aritmética). Para qualquer um desses sistemas, sempre haverá afirmações sobre os números naturais que são verdadeiras, mas que não podem ser provadas dentro do sistema. O segundo teorema da incompletude, uma extensão do primeiro, mostra que tal sistema não pode demonstrar sua própria consistência.
-
Teorema 1: “Qualquer teoria axiomática recursivamente enumerável e capaz de expressar algumas verdades básicas de aritmética não pode ser, ao mesmo tempo, completa e consistente. Ou seja, sempre há em uma teoria consistente proposições verdadeiras que não podem ser demonstradas nem negadas.”
-
Teorema 2 : “Uma teoria, recursivamente enumerável e capaz de expressar verdades básicas da aritmética e alguns enunciados da teoria da prova, pode provar sua própria consistência se, e somente se, for inconsistente.”
Máquinas de Turing
A Máquina de Turing é um arcabouço teórico concebido pelo matemático britânico Alan Turing (1912-1954).Em um sentido preciso, é um modelo abstrato de um computador, que se restringe apenas aos aspectos lógicos do seu funcionamento (memória, estados e transições), e não a sua implementação física. Turing provou que para qualquer sistema formal existe uma máquina de Turing que pode ser programada para imitá‐lo. Era este sistema formal genérico, com a habilidade de imitar qualquer outro sistema formal, o que Turing procurava essencialmente. Tais sistemas chamam‐se Máquinas de Turing Universais. O lógico matemático Alonzo Church chegou a definir: “Qualquer processo aceito por nós homens como um algoritmo é precisamente o que uma máquina de Turing pode fazer”.
Sendo assim, uma máquina de Turing consiste em:
-
Uma fita, dividida em células, uma adjacente à outra. Cada célula contém um símbolo de algum alfabeto finito. O alfabeto contém um símbolo especial branco (aqui escrito como ¬) e um ou mais símbolos adicionais. Assume-se que a fita é arbitrariamente extensível para a esquerda e para a direita, isto é, a máquina de Turing possui tanta fita quanto é necessário para a computação. Assume-se também que células que ainda não foram escritas estão preenchidas com o símbolo branco.
-
Um cabeçote, que pode ler e escrever símbolos na fita e mover-se para a esquerda ou para a direita. Um registrador de estados, que armazena o estado da máquina de Turing. O número de estados diferentes é sempre finito e há um estado especial denominado estado inicial com o qual o registrador de estado é inicializado.
-
Uma tabela de ação (ou função de transição) que diz à máquina que símbolo escrever, como mover o cabeçote (que pode movimentar-se para esquerda e para a direita) e qual será seu novo estado, dados o símbolo que ele acabou de ler na fita e o estado em que se encontra. Se não houver entrada alguma na tabela para a combinação atual de símbolo e estado então a máquina para.
Note que cada parte da máquina é finita e sua quantidade de fita potencialmente ilimitada dá uma quantidade ilimitada de espaço de memória.
Definição formal ( Máquina de Turing com uma fita)
Mais formalmente, uma máquina de Turing (com uma fita) é usualmente definida como uma Tupla \(M=(Q,\Sigma, \Gamma, s, b, F, \delta)\), onde
\(Q\) é um conjunto finito de estados \(\Sigma\) é um alfabeto finito de símbolos \(\Gamma\) é o alfabeto da fita (conjunto finito de símbolos) \(s \in Q\) é o estado inicial \(b \in \Gamma\) é o símbolo branco (o único símbolo que se permite ocorrer na fita infinitamente em qualquer passo durante a computação) \(F \subseteq Q\) é o conjunto dos estados finais \(\delta: Q \times \Gamma ⇒ Q \times \Gamma \times \{\leftarrow,\rightarrow\}\) é uma função parcial chamada função de transição, onde \(\leftarrow\) é o movimento para a esquerda e \(\rightarrow\) é o movimento para a direita.
Definições na literatura às vezes diferem um pouco, para tornar argumentos ou provas mais fáceis ou mais claras, mas isto é sempre feito de maneira que a máquina resultante tem o mesmo poder computacional. Por exemplo, mudar o conjunto \(\{\leftarrow,\rightarrow\}\) para \(\{\leftarrow,\rightarrow,P\}\), onde \(P\) permite ao cabeçote permanecer na mesma célula da fita em vez de mover-se para a esquerda ou direita, não aumenta o poder computacional da máquina [1].
Decidibilidade
Como já dito anteriormente, a proposta de Hilbert era reduzir toda matemática a manipulações reais e responder afirmativamente às seguintes questões. A matemática é completa? É consistente? É decidível?
A tese de Church-Turing, quando particularizada para problemas de decisão, poderia ser assim enunciada: se um problema de decisãoo tem solução, então existe uma MT que o soluciona. Dessa forma, para mostrar que um problema de decisão não tem solução, basta mostrar que não existe \(MT\) que o soluciona. Por outro lado, dada a equivalência dos diversos formalismos, um problema de decisão não tem solução se não for possível expressar uma solução em qualquer um dos mesmos. Assim, por exemplo, se não existir um algoritmo que seja uma solução para um problema de decisão, então esse problema de decisão é insolúvel.
Compreender se a matemática é decidivel ficou conhecido como “O Problema de Decisão de Hilbert” (Hilbert’s Entscheidungsproblem): encontrar um mecanismo genérico que, ao considerar um enunciado qualquer formulado em Lógica de Primeira Ordem, fosse capaz de verificar sua validade ou não. Tanto Church quanto Turing demonstraram que, em seus respectivos modelos de computação, que o Entscheidungsproblem é indecidível, ou seja: não existe uma máquina de Turing ou uma função no cálculo lambda capaz de determinar se uma proposição arbitrária em lógica de primeira ordem é verdadeira
Diversos outros problemas foram demonstrados indecidíveis nesses modelos de computação. Um exemplo clássico é o problema da parada, que consiste em determinar se a execução de uma dada máquina de Turing termina em um número finito de passos para uma dada entrada ou, analogamente, se uma dada fórmula em cálculo lambda possui uma forma normal. A importância de Tese de Church-Turing reside no fato de que, se a máquina de Turing representa adequadamente o que é efetivamente calculável, os limites que a máquina de Turing é capaz de alcançar representam limites teóricos de computabilidade dos quais, em tese, não poderíamos escapar.
Entender quando um problema é algoritmicamente insolúvel é útil pois torna o cientista da computação apto a simplificar ou alterar o problema antes que possa encontrar uma solução algoritmica. Como qualquer ferramenta os computadores tem capacidades e limitações que devem ser reocnhecidas caso deseje-se fazer pleno uso dos seus poderes computacionais.
O Problema da Parada (Halting Problem)
Uma característica importante de qualquer um dos formalismos citados é o que se denomina auto-referência. Por exemplo, é possível ter MTs que manipulam MTs: para isso, basta codificar (ou representar) a MT a ser manipulada, usando-se um alfabeto apropriado, antes de supri-la como entrada. Essa característica propicia a possibilidade de se construir uma máquina universal, ou seja, uma MT (ou programa em uma linguagem de programação) que seja capaz de simular uma MT (programa) qualquer suprida como argumento. A possibilidade de auto-referência é uma caracterísstica fundamental que levou à descoberta de funções não computáveis, a mais famosa delas é o Halting Problem ou Problema da Parada
Na teoria da computabilidade, o problema da parada constitui um dos teoremas mais importantes filosoficamente da teoria da computação: existe um problema especifico que é algoritmicamente insolúvel. O experimento mental do problema da parada é um problema de decisão que pode ser declarado informalmente da seguinte forma:
“Dadas uma descrição de um programa e uma entrada finita, decida se o programa termina de rodar ou rodará indefinidamente.”
Ou seja, dadas uma \(MT\) arbitrária \(M\) e uma cadeia arbitrária \(w\), determinar se a computação de \(M\) com a entrada \(w\) para
Formalmente o problema é dado por:
\begin{align} A_{MT} = { \ [M,w] \ | \ M \ é \ uma \ MT \ e \ M \ aceita \ w } \end{align}
Para mostrar que \(MT\) é turing-decidivel, precisamos construir uma \(MT\) que quando recebe um \([M,w]\) qualquer, decide se \([M,w] \in A_{MT}\) ou \([M,w] \notin A_{MT}\).
Note que temos uma máquina \(M\) que recebe um cadeia \(w\). Se a máquina \(M\) aceita a cadeia \(w\), a cadeia pertence àquela linguagem e \(M\) aceita \(w\), caso contrário, ela não pertence a cadeia dada e \(M\) não aceita \(w\). Aceitar \(w\) aqui implica que \(M\) entrou em estado de aceitação, já não aceitar, implica que \(M\) não entrou em estado de aceitação, que por sua vez significa que \(M\) ou entrou em estado de rejeição ou não entrar em nenhum estado de parada. Logo dizemos que \(M\), ao não aceitar uma cadeia pode tanto entrar em estado de rejeição quanto em loop.
Assim, precisamos agora de uma nova máquina \(MT\) se a máquina anterior \(M\) para ou não ao receber uma cadeia. Então considere:
\(U =\) “Sobre a entrada \([M,w]\), onde \(M\) é uma MT e \(w\) uma cadeia”:
- Simule \(M\) sobre \(w\)
- Se \(M\) entra no estado de aceitação, aceite; Se \(M\) entra no estado de rejeição, rejeite
\(U\) é uma máquina universal – Dado que \(U\) é uma Máquina de Turing que simula máquinas de Turing.
Como vimos anteriormente,a possibiliade de \(M\) não rejeitar a cadeia \(w\) ou nunca entrar em um estado de parada faz com que \(U\) também nunca entre em um estado de aceitação ou rejeiçao. Logo, caso seja passada uma cadeia que pertence a linguagem \(U\) entrará em aceitação, caso seja passada uma cadeia que não pertence àquela linguagem não é possível estimar uma saida predeterminada. Assim, \(U\) não decide uma linguagem mas a reconhece (\(U\) é Turing-reconhecivel).
Seria \(U\) Turing-decidível ?
Relembrando o teorema:
\begin{align} A_{MT} = { \ [M,w] \ | \ M \ é \ uma \ MT \ e \ M \ aceita \ w } \end{align}
Por contradição, podemos supor que \(A_{MT}\) é Turing-decidível.
Seja \(H\) um decisor para \(A_{MT}\), temos:

Agora sobre a máquina \(H\), construiremos uma nova máquina a qual chamaremos de \(D\). Então considere:
\(D =\) “Sobre a entrada \([M]\)”:
- Execute \(H\) sobre \([M,[M]]\)
- Se \(H\) aceita, rejeite; Se \(H\) rejeita, aceite
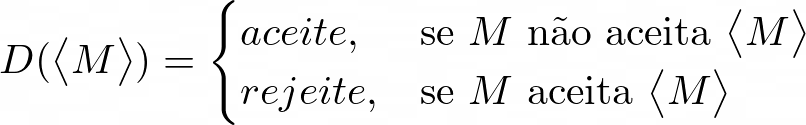
Trata-se de executar um programa utilizando o próprio programa chamador como entrada, algo que de fato ocorre com frequencia no mundo da programação.
Por exemplo:
Um compilador é um programa que traduz outros programas. Um compilador para a liguangem C pode também ser escrito em C, portanto rodar esse programa sobre si próprio. Ou ainda podemos levar em consideração a existência de interpretadores em python para para algoritmos escritos em python
Então resumindo o que temos até agora:
Temos uma decisor \(H\) que recebe uma máquina \(M\) e uma cadeia \(w\). \(H\) decide essa linguagem entrando em estado de aceitação quando \(M\) aceita \(w\), e entra em estado de rejeição quando \(M\) não aceita \(w\).
\(D\) por sua vez, recebe uma única máquina \(H\) e entra em estado de aceitação quando \(M\) não aceita a própria representação \([M]\), entra em estado de rejeição quando \(M\) aceita a própria representação \([M]\)
| \([M_{1}]\) | \([M_{2}]\) | \([M_{3}]\) | \([M_{4}]\) | … | |
|---|---|---|---|---|---|
| \([M_{1}]\) | \(aceite\) | \(rejeite\) | \(aceite\) | \(rejeite\) | … |
| \([M_{2}]\) | \(aceite\) | \(aceite\) | \(aceite\) | \(aceite\) | … |
| \([M_{3}]\) | \(rejeite\) | \(rejeite\) | \(rejeite\) | \(rejeite\) | … |
| \([M_{4}]\) | \(aceite\) | \(aceite\) | \(rejeite\) | \(rejeite\) | … |
| … | … | … | … | … | … |
Considerando a tabela acima observe que quando passamos a represetação de \([M_{1}]\) para a máquina \(M_{1}\). Já no caso de passarmos a representação \([M_{2}]\) para a máquina \(M_{1}\) ela entra no estado de rejeição. Ou seja, ao passarmos para o decisor \(H\) na maquina \(M_{1}\) a representação de \([M_{1}]\), o decisor entrará em estado de aceitação – \(H([M_{1},[M_{1}]])\). Isso porque, como vimos na tabela acioma \(M_{1}\) aceita a representação \([M_{1}]\). O mesmo não acontece caso passemos a representação de \([M_{2}]\) para \(M_{1}\) – \(H([M_{1},[M_{2}]])\), o que faz com que o decisor \(H\) entre em estado de rejeição.
Podemos utilizar o raciocínio equivalente para o decisor \(D\). Porém, nesse caso, ao passarmos a representação \([M_{1}]\) para \(M_{1}\) ela é aceita, e por definição, vimos que em \(D\), caso uma máquina aceite sua própria definição ela entrará em estado de rejeição – \(D([M_{1}])\). Caso façamos o mesmo procedimento mas desta vez considerando a representação \([M_{3}]\), ou seja, \(M_{3}\) recebendo a sua própria representação \([M_{3}]\) – \(D([M_{3}])\) – a mesma não é aceita e assim \(D\) entra em estado de aceitação.
Mas o que acontece quando rodamos \(D\) com sua própria representaçao \([D]\) ?
Subistituindo no formalismo temos a seguinte definição:
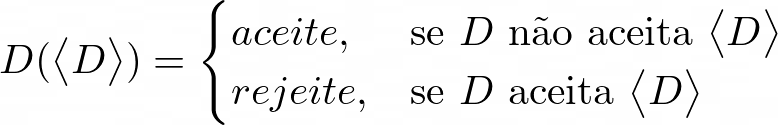
\(D\) vai aceitar sua própria descrição \([D]\) quando não aceita sua própria descrição. E vai rejeitar sua própria descrição, quando aceitar sua própria descrição. Como \(D\) também é a representação de uma máquina podemos ver isso na tabela abaixo:
| \([M_{1}]\) | \([M_{2}]\) | \([M_{3}]\) | \([M_{4}]\) | … | \([D]\) | |
|---|---|---|---|---|---|---|
| \([M_{1}]\) | \(aceita\) | \(rejeita\) | \(aceita\) | \(rejeita\) | … | |
| \([M_{2}]\) | \(aceita\) | \(aceita\) | \(aceita\) | \(aceita\) | … | |
| \([M_{3}]\) | \(rejeita\) | \(rejeita\) | \(rejeita\) | \(rejeita\) | … | |
| \([M_{4}]\) | \(aceita\) | \(aceita\) | \(rejeita\) | \(rejeita\) | … | |
| \(D\) | \(rejeita\) | \(rejeita\) | \(aceita\) | \(aceita\) | … | |
| … | … | … | … | … | … | ??? |
\(D\), por assim dizer, acaba fazendo exatamenteo contrário do que fazem as máquinas \(M_{n}\) ao receber suas próprias representações. Ou seja, independentemente do que \(D\) faz, ela é forçada a fazer o oposto, o que obviamente é um paradoxo. Consequentemente nem \(D\) nem \(H\) podem existir, e assim dizemos que não existe uma máquina de Turing que decida a linguangem \(A_{MT}\). Logo, podemos concluir que:
\begin{align} \text{Teorema}: \ A_{MT} \ \text{é indecidível}. \end{align}
Alan Turing provou em 1936 que um algoritmo genérico para resolver o problema da parada para todos pares programa-entrada possíveis não pode existir. Assim, dizemos que o problema da parada é indecidível nas Máquinas de Turing.
A importância histórica do problema da parada reside no fato de que foi um dos primeiros problemas a ser provado indecidível. (A prova de Turing foi lançada em maio de 1936, enquanto a prova de Alonzo Church da indecidibilidade de um problema no cálculo lambda já havia sido lançada em abril de 1936). Subsequentemente, muitos outros problemas foram descritos; o método típico de provar que um problema é indecidível é a técnica de redução. Para isso, o cientista da computação mostra que se uma solução para o novo problema foi encontrada, ela poderia ser usada para decidir um problema indecidível (transformando instâncias do problema indecidível em instâncias do novo problema).
Outra consequência da indecidibilidade do problema da parada é o Teorema de Rice que enuncia que a verdade de qualquer enunciado não-trivial sobre a função definida por um algoritmo é indecidível. Então, por exemplo, o problema da parada “esse algoritmo parará para a entrada 0” já é indecidível. Perceba que esse teorema considera a função definida pelo algoritmo e não o algoritmo propriamente dito. É, por exemplo, possível decidir se um algoritmo vai parar dentro de 100 passos, mas isso não é um enunciado sobre a função, definida pelo algoritmo.
Devido ao fato de que a resposta negativa ao problema da parada demonstra que existem problemas que não podem ser resolvidos por máquinas de Turing, a tese de Church-Turing limita o que pode ser atingido por qualquer máquina que implemente métodos efetivos. Porém, nem todas as máquinas imagináveis são sujeitas à tese de Church-Turing (Máquinas Oráculo não são).
Ainda não se pode afirmar se é possível ou não existir um processo físico determinístico que a longo prazo possa contornar uma simulação por máquina de Turing, desta forma, também é relevante saber se este processo hipotético pode ter utilidade na forma de uma máquina calculadora (um hipercomputador) que poderia resolver o problema da parada para uma máquina de Turing, assim como outras coisas. Também se pergunta se qualquer um destes processos físicos desconhecidos estão envolvidos no funcionamento do cérebro humano e se humanos podem resolver o problema da parada [3].
A introdução de Turing do modelo de máquina que posteriormente ficou conhecido como Máquinas de Turing, introduzido no artigo, provou-se um modelo muito conveniente para a Teoria da Computação.
O Método da Diagonalização
A prova da indecibilidade do problema da parada usa uma técnica chamada diagonalização, descoberta pelo matemático George Cantor em 1873. Cantor estava preocupado com o problema de se medir os tamanhos de conjuntos infinitos.
Se existirem dois conjuntos infinitos, como podemos afirmar que um conjunto é maior que o outro ou que os dois conjuntos tem o mesmo tamanho?
Por mais absurdo que pareça a idéia era responder a seguinte questão:
Será que existem infinitos que são tão grandes ou maiores que outros infinitos?
Para conjunjuntos finitos, é claro, responder a essas questões é algo trivial. Porém, estimar o número de elementos de dois conjuntos infinitos torna-se uma tarefa mais difícil.
Cantor propôs uma solução elegante para esse problema. Ele observou que dois conjuntos finitos têm o mesmo tamanho se os elementos de um deles puder ser emparelhado com os elementos do outro conjunto. Esse método compara os tamanhos sem recorrer a contagem, logo, podemos estender essa idéia para conjuntos infinitos.
Por definição temos:
Suponha que tenhamos os conjuntos \(A\) e \(A\) e uma função \(f\) de \(A\) para \(B\). Digamos ainda que função \(f\) é um-para-um se ela nunca mapeia dois elementos diferentes para um mesmo lugar – ou seja, se \(f(a) \neq f(b)\) sempre que \(a \neq b\). Digamos que \(f\) é sobrejetora se ela atinge todo elemento de \(B\) – ou seja, se para todo \(b \in B\) existe um \(a \in A\) tal que \(f(a) = b\). Consideremos que \(A\) e \(B\) são do mesmo tamanho se existe uma função um-para-um e sobrejetora \(f : A \rightarrow B\). Logo, uma função que é tanto um-para-um quanto sobrejetora é denominada uma correspondência. Em uma correspondência, todo elemento de \(A\) é mapeado para um único elemento de \(B\) e cada elemento de \(B\) tem uma único elemento de \(A\) mapeado para ele.
Assim, uma correspondência é simpelemente uma maneira de emparelhar os elementos de \(A\) com os elementos de \(B\).
Podemos entender essa definição através do seguinte exemplo:
Seja \(N\) o conjunto dos números naturais \({1,2,3,...}\) e suponha que \(\varepsilon\) seja o conjunto dos números naturais pares \({2,4,6,...}\). Usandoa definição de Cntor de tamanho podemos ver que \(N\) e \(\varepsilon\) têm o mesmo tamanho. A correspondência \(f\) mapeando \(N\) para \(\varepsilon\) é simplesmente \(f(n)=2n\). Podemos visualizar \(f\) mais facilmente com a ajuda de uma tabela:
| \(n\) | \(f(n)\) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| … | … |
Logo temos a seguinte definição:
Um conjunto \(A\) é contável se é finito ou se tem o mesmo tamanho de \(N\).
Comparação com máquinas reais
Frequentemente diz-se que as máquinas de Turing, ao contrário de autômatos mais simples, são tão poderosas quanto máquinas reais, e são capazes de executar qualquer operação que um programa real executa. O que está faltando neste enunciado é que praticamente qualquer programa particular executando em uma máquina particular e dada uma entrada finita é, na verdade, nada além de um autômato finito determinístico, já que a máquina em que executa pode estar apenas em uma quantidade finita de configurações.
Máquinas de Turing poderiam de fato ser equivalentes a uma máquina que tenha uma quantidade ilimitada de espaço de armazenamento. Podemos questionar então por que as máquinas de Turing são modelos úteis de computadores reais. Há várias maneiras de responder a isto:
-
A diferença está apenas na habilidade de uma máquina de Turing de manipular uma quantidade ilimitada de dados. No entanto, dada uma quantidade finita de tempo, uma máquina de Turing (tala qual uma máquina real) pode apenas manipular uma quantidade finita de dados.
-
Como uma máquina de Turing, uma máquina real pode ter seu espaço de armazenamento aumentado conforme a necessidade, através da aquisição de mais discos ou outro meio de armazenamento. Se o suprimento destes for curto, a máquina de Turing pode se tornar menos útil como modelo. Mas o fato é que nem as máquinas de Turing, nem as máquinas reais precisam de quantidades astronômicas de espaço de armazenamento para fazer a maioria das computações que as pessoas normalmente querem que sejam feitas. Frequentemente o tempo de processamento requerido é o maior problema.
-
Máquinas reais são muito mais complexas que uma máquina de Turing. Por exemplo, uma máquina de Turing descrevendo um algoritmo pode ter algumas centenas de estados, enquanto o autômato finito determinístico equivalente em uma dada máquina real tem quadrilhões.
-
Máquinas de Turing descrevem algoritmos independentemente de quanta memória eles utilizam. Há um limite máximo na quantidade de memória que qualquer máquina que conhecemos tem, mas este limite pode crescer arbitrariamente no tempo. As máquinas de Turing nos permitem fazer enunciados sobre algoritmos que (teoricamente) valerão eternamente, independentemente dos avanços na arquitetura de computadores convencionais.
-
Máquinas de Turing simplificam o enunciado de algoritmos. Algoritmos executando em máquinas abstratas equivalentes a Turing são normalmente mais gerais que suas contrapartes executando em máquinas reais, porque elas têm tipos com precisão arbitrária disponíveis e nunca precisam tratar condições inesperadas (incluindo, mas não somente, acabar a memória).
Uma perspectiva em que máquinas de Turing são consideradas abstrações mais elementares para programas é o fato que muitos programas reais, tais como sistemas operacionais e processadores de texto, são escritos para receber entradas irrestritas através da execução, e, portanto, não param. Máquinas de Turing não modelam bem tal “computação contínua” (mas ainda podem modelar porções dela, tais como procedimentos individuais).
Outra limitação de máquinas de Turing é que elas não modelam a organização estrita de um problema específico. Por exemplo, computadores modernos são, na verdade, instâncias de uma forma mais específica de máquina de computação, conhecido como máquina de acesso aleatório. A principal diferença entre esta máquina e a máquina de Turing é que esta utiliza uma fita infinita, enquanto a máquina de acesso aleatório utiliza uma sequência indexada numericamente (tipicamente um campo inteiro). O resultado desta distinção é que há otimizações computacionais que podem ser executadas baseadas nos índices em memória, o que não é possível em uma máquina de Turing geral. Assim, quando máquinas de Turing são utilizadas como base para tempo de execuções restritos, um “falso limite inferior” pode ser provado em determinados tempos de execução de algoritmos (graças à premissa falsa de simplificação da máquina de Turing). Um exemplo disto é uma “ordenação por contagem”, o que aparentemente viola o limite inferior (n log n) em algoritmos de ordenação.
Máquinas de Turing determinísticas e não-determinísticas
Se a tabela de ação tem no máximo uma entrada para cada combinação de símbolo e estado, então a máquina é uma máquina de Turing determinística (MTD). Se a tabela de ação contém múltiplas entradas para uma combinação de símbolo e estado, então a máquina é uma máquina de Turing não-determinística (MTND ou MTN).
Máquina de Turing Não-Determinística (MNT)
Uma máquina de Turing não determinística é um tipo teórico de computador no qual comandos específicos podem permitir uma série de ações, em vez de um comando específico que leva a apenas uma ação permitida no modelo determinístico de computação. Onde a programação determinística é uma condição simples de ‘entrada \(X\) leva à ação \(Y\)’, uma configuração de máquina de Turing não determinística teoricamente permitiria que a entrada \(X\) levasse a uma variedade de ações Y(array) Máquinas de Turing não determinísticas podem realmente fornecer uma direção para o futuro da computação inteligente ou artificialmente inteligente. Ao desatar o trabalho computacional do paradigma determinístico, os computadores poderiam aprender a resolver problemas mais complicados e ‘pensar’ mais como humanos. Um tipo de máquina de Turing não-determinística é a máquina de Turing probabilística. Aqui, o conjunto de ações (\(Y\)) mencionado acima é determinado por meio de alguma distribuição de probabilidade. Outra maneira de dizer isso é que quando a máquina tem mais de uma escolha, ela vai para um modelo probabilístico, analisa esse modelo e faz uma escolha de acordo. Existem muitas outras maneiras de ordenar uma máquina de Turing não determinística, mas o princípio é que o computador precisa escolher entre um conjunto de opções disponíveis. Alguns modelos de Turing não determinísticos em uma configuração de aprendizado de máquina podem consistir no computador seguindo caminhos de lógica para um final aceito ou rejeitado e, em seguida, voltando e escolhendo uma ação de acordo.
Algoritmos Determinísticos e Não Determinísticos
Em um algoritmo determinístico, para uma determinada entrada em particular, o computador sempre produzirá a mesma saída passando pelos mesmos estados, mas no caso do algoritmo não determinístico , para a mesma entrada, o compilador pode produzir saídas diferentes em execuções diferentes. De fato, algoritmos não determinísticos não podem resolver o problema em tempo polinomial e não podem determinar qual é o próximo passo. Os algoritmos não determinísticos podem mostrar diferentes comportamentos para a mesma entrada em diferentes execuções e há um grau de aleatoriedade nisso.
| Algoritmo Determinístico | Algoritmo não-determinístico |
|---|---|
| Para uma determinada entrada, o computador fornecerá sempre a mesma saída. | Para uma determinada entrada, o computador fornecerá diferentes saídas em diferentes execuções. |
| Pode resolver o problema em tempo polinomial. | Não é possível resolver o problema em tempo polinomial |
| Pode determinar o próximo passo de execução. | Não é possível determinar a próxima etapa de execução devido a mais de um caminho que o algoritmo pode seguir. |
Medidas de complexidade e Máquinas de Turing
Para uma definição precisa do que significa resolver um problema usando uma determinada quantidade de tempo e espaço, é utilizado um modelo computacional como a máquina de Turing determinística . O tempo requerido por uma máquina de Turing determinística \(M\) na entrada \(x\) é o número total de transições de estado, ou etapas, que a máquina faz antes de parar e emitir a resposta (“sim” ou “não”). Diz-se que uma máquina de Turing \(M\) opera dentro do tempo \(f(n)\) se o tempo requerido por \(M\) em cada entrada de comprimento n for no máximo \(f(n)\). Um problema de decisão A pode ser resolvido a tempo \(f(n)\) se existe uma máquina de Turing operando no tempo \(f(n)\) que resolve o problema. Como a teoria da complexidade está interessada em classificar problemas com base em sua dificuldade, define-se conjuntos de problemas com base em alguns critérios. Por exemplo, o conjunto de problemas solucionáveis no tempo \(f(n)\) em uma máquina de Turing determinística é então denotado por \(DTIME (f(n))\).