Ajustando hiperparâmetros em Redes Neurais Convolucionais utilizando Otimização Bayesiana.

Os algorítmos de aprendizado de máquina raramente estão livres de parametrização, normalmente tais parâmetros controlam a taxa de aprendizado ou as capacidades do modelo subjacente. Esses parâmetros são frequentemente considerados incômodos, tornando atraente o desenvolvimento de algoritmos de aprendizado de máquina que sejam capazes de manipula-los de forma mais simples e objetiva. Logo, uma abordagem mais flexível sobre esse problema é visualizar a otimização de tais parâmetros como um procedimento a ser automatizado.

Algoritmos de aprendizado de máquina, no entanto, têm certas características que os diferenciam de outros problemas de otimização menos explicitos, exigindo do modelo uma quantidade variável de tempo. Por exemplo, treinar uma pequena rede neural com 10 unidades ocultas levará menos tempo do que uma rede maior com 1000 unidades ocultas.

Através de uma abordagem dita “caixa preta”, é posível considerar o ajuste desses parâmetros como o processo de otimização de uma função desconhecida, e assim invocar algoritmos desenvolvidos para esse fim. Uma boa escolha é otimização bayesiana, que demonstrou superar outros algoritmos de otimização global de ponta em várias funções desafiadoras de benchmark de otimização.

Para funções contínuas, a otimização bayesiana normalmente funciona assumindo que a função desconhecida foi amostrada de um processo gaussiano e mantém uma distribuição posterior para essa função à medida que as observações são feitas ou, no nosso caso, como são observados os resultados da execução de experimentos com algoritmos de aprendizado com diferentes hiperparâmetros.

Mas antes vamos entender brevemente o que são processos gaussianos.

Processos Gaussianos

Uma das grandes vantagens do aprendizado de máquina é estimar funções com relações complexas entre variáveis lineares e não lineares. Se quisermos encarar problemas mais complexos com modelos lineares simples, podemos extender a forma funcional estimada adicionando mais parâmetros, o que pode ser obtido, por exemplo, através uma expansão polinomial. A idéia geral é aumentar o grau do polinômio estimado, tornando-o arbitrariamente complexo, para então conseguir ajusta-lo a dados não lineares.

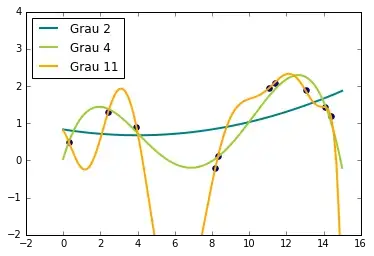
E se não quisermos especificar previamente o número de parâmetros do modelo?

Uma possibilidade é ampliar o escopo e considerar todas as funções que se encaixam nos nossos dados, cada uma com sua infinidade de parâmetros necessários. Processos Gaussianos lidam diretamente com esse cenário. Um processo gaussiano é um modelo estatístico em que as observações ocorrem em um domínio contínuo, por exemplo, tempo ou espaço. Em um processo gaussiano, cada ponto em algum espaço de entrada contínua está associada com uma variável aleatória e com a distribuição normal. A distribuição de um processo gaussiano é a distribuição conjunta de todas as infinitas variáveis aleatórias, e como tal, é uma distribuição de funções com um domínio contínuo.

Processos Gaussianos são modelos probabilísticos ou bayesianos, isso significa que, além de nos fornecer uma estimativa pontual de uma previsão (geralmente a média condicional), os processos gaussianos também especificam toda a distribuição preditiva a posteriori, tornando a obtenção de estatísticas de incerteza algo natural. Isso é extremamente importante para aplicações de aprendizado de máquina em cenários de alto risco, como medicina, carros autônomos ou concessão de crédito. Nessas áreas, além da previsão, estamos frequentemente interessados no grau de certeza do modelo para que, caso ele seja muito alto, possamos passar a decisão para um especialista humano.

Otimização Bayesiana

A otimização bayesiana é uma estratégia poderosa para encontrar extremos de funções objetivas que são caras de avaliar. Em verdade a otimização bayesiana é aplicável em situações em que não existe uma forma fechada para a função objetivo, mas é possível obter observações (possivelmente ruidosas) dessa função em valores amostrados. Logo esse tipo de otimização torna-se particularmente útil quando essas avaliações são caras quando não se tem acesso a derivativos ou quando o problema em questão é não convexo.

Explico. A otimização bayesiana funciona construindo uma distribuição posterior de funções (processo gaussiano) que melhor descreve a função que você deseja otimizar. À medida que o número de observações aumenta, a distribuição posterior melhora — Teorema do Limite Central — e o algoritmo torna-se mais certo de quais regiões no espaço de parâmetros valem a pena explorar e quais não, como visto na figura abaixo.

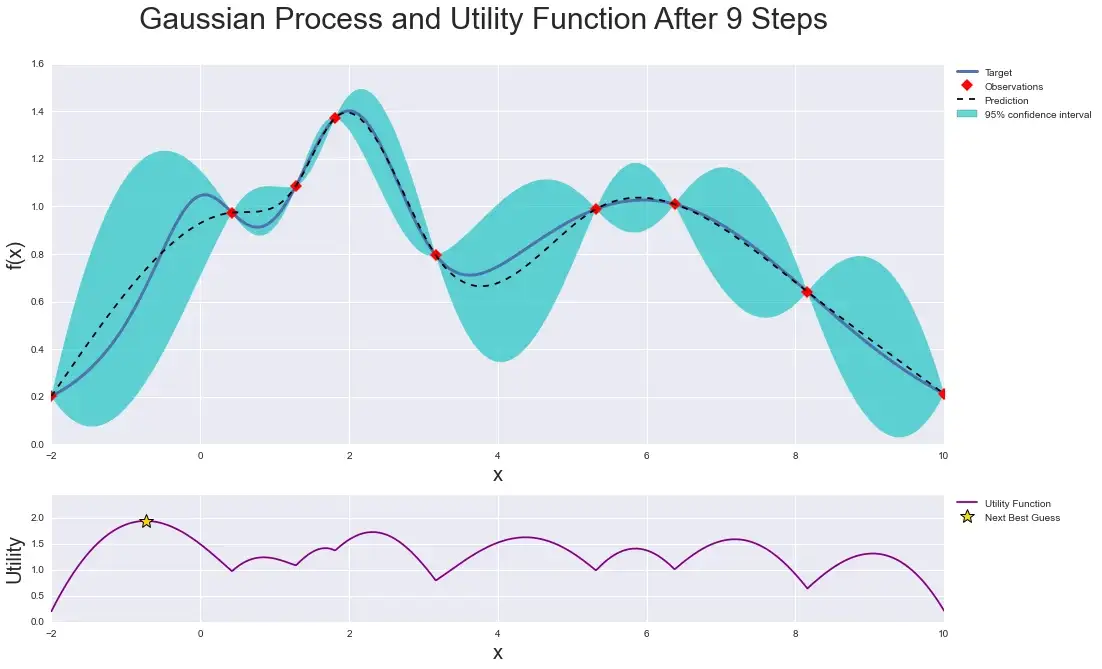
À medida que você repete continuamente a construção dessas funções, o algoritmo equilibra suas necessidades de exploração, levando em consideração o que sabe sobre a função de destino. Em cada etapa, um processo gaussiano é ajustado às amostras conhecidas (pontos explorados anteriormente), e a distribuição posterior, combinada com uma estratégia de exploração (Limite de Confiança Superior ou Melhoria Esperada), são usadas para determinar o próximo ponto que deve ser explorado.

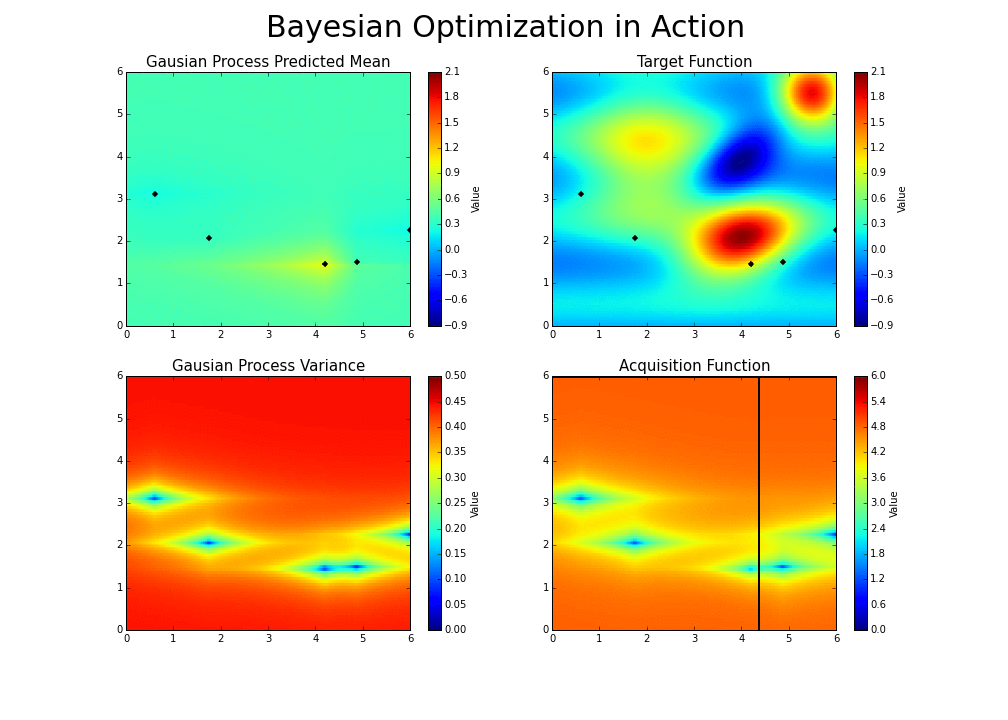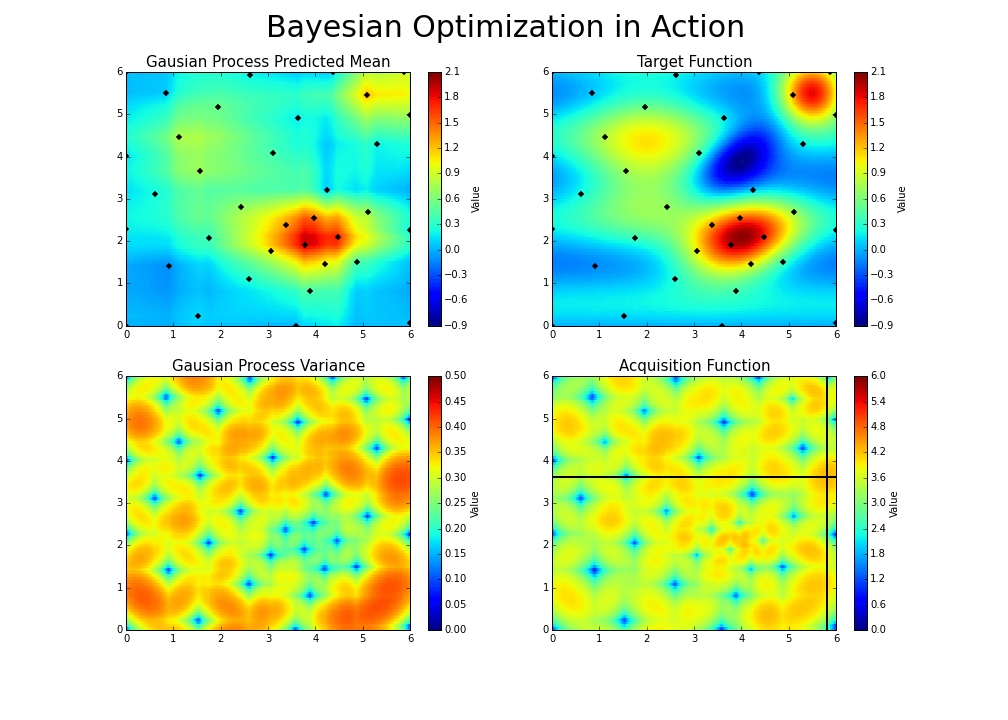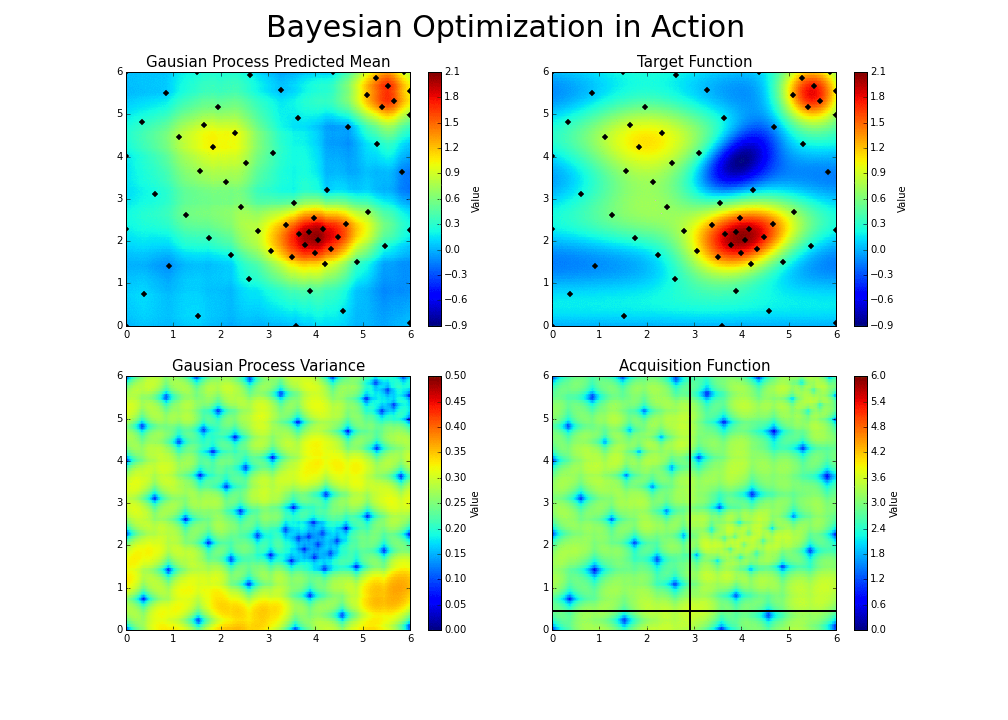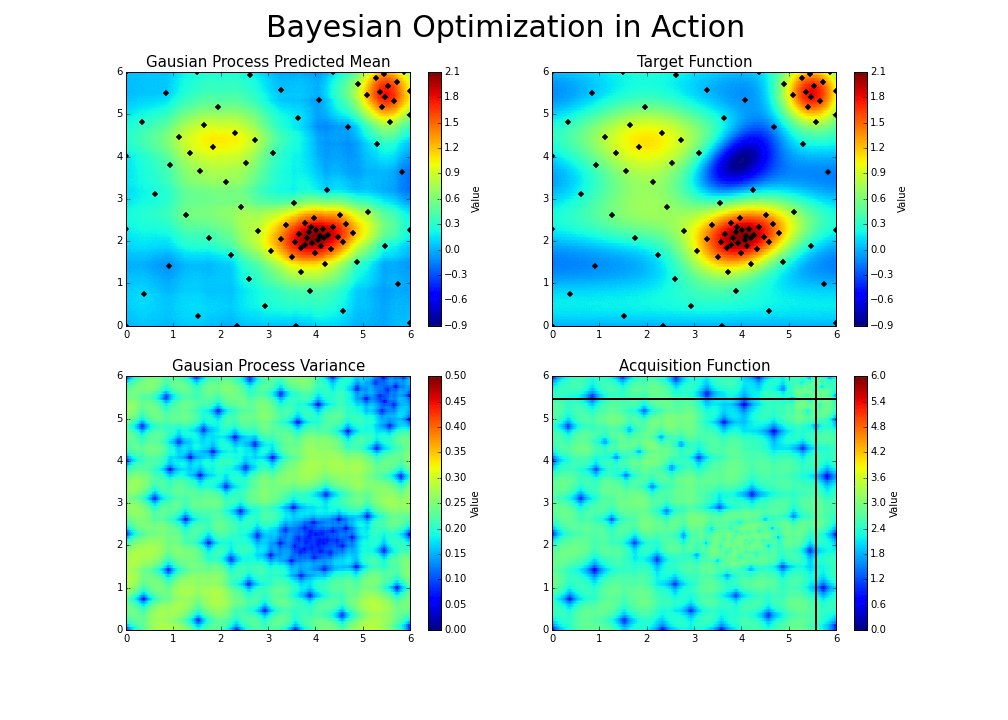
Como em outros tipos de otimização, na otimização bayesiana, estamos interessados em encontrar o mínimo de uma função \(f(x)\) em algum conjunto limitado \(X\). Esse processo é projetado para minimizar o número de etapas necessárias para encontrar uma combinação de parâmetros próximos à combinação ideal. Para fazer isso, esse método usa um problema de otimização de proxy (encontrando o máximo da função de aquisição) que, embora ainda seja um problema difícil, é mais barato (no sentido computacional) e ferramentas comuns podem ser empregadas. Portanto, a otimização bayesiana é mais adequada para situações em que a amostragem da função a ser otimizada é um empreendimento muito caro. Assim, o que torna a otimização bayesiana diferente de outros procedimentos é que ela constrói um modelo probabilístico para \(f(x)\) e depois explora esse modelo para tomar decisões sobre onde X deve avaliar a função, para em seguida definir um possível modelo final.

Alguns estudos exploraram várias estratégias para otimizar os hiperparâmetros dos algoritmos de aprendizado de máquina. Eles demonstraram que estratégias como o Grid Search são inferiores a Random Search e recomendam o uso da otimização bayesiana com os processos gaussianos. Isso deve-se ao fato de que ao contrário do Grid Search, na otmização bayesiana nem todos os valores dos parâmetros são testados, mas um número fixo de configurações de parâmetros é amostrado das distribuições especificadas.

Otimização Bayesiana na prática

Todo o código apresentado está diponível aqui

A seguir vamos aplicar a otimização bayessiana na prática. No entanto vamos aplica-la a uma rede neural convolucional e tentar o obter alguns hiperparâmetros que otimizem a nossa tarefa de classificação.

O pacote de otimização bayesiana que vamos usar é o BayesianOptimization, que pode ser instalado com o seguinte comando:

pip install bayesian-optimization

Em nosso experimento, a função recebe um conjunto de valores de hiperparâmetros como entradas e devolve como resultado a precisão estimada para o nosso otimizador Bayesiano. Dentro da função, um novo modelo será construído com os hiperparâmetros especificados, treinado para várias épocas e avaliado com base nas métricas definidas. Cada nova precisão avaliada se tornará uma nova observação para o otimizador bayesiano, que contribui para os próximos valores dos hiperparâmetros pesquisados.

Primeiramente vamos criar uma função que retorna nosso dataset utilizando uma estratégia de batches.

Se você não sabe como funciona essa estratégia, pode encontrar nesse artigo aqui uma breve explicação de como utiliza-la e porquê ele é importante.

Para o nosso dataset utilizemos o MNIST, um conjunto de dados composto por 60.000 imagens de dígitos manuscritos. Os dígitos já vem normalizados em tamanho e centralizados em uma imagem de tamanho fixo.

NUM_CLASSES = 10
def get_input_datasets(use_bfloat16=False):
 
 # input image dimensions
 img_rows, img_cols = 28, 28
 cast_dtype = tf.bfloat16 if use_bfloat16 else tf.float32

 # the data, split between train and test sets
 (x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

 if tf.keras.backend.image_data_format() == 'channels_first':
    x_train     = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
    x_test      = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
    input_shape = (1, img_rows, img_cols)
 else:
    x_train     = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
    x_test      = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
    input_shape = (img_rows, img_cols, 1)
    x_train     = x_train.astype(‘float32’)
    x_test      = x_test.astype(‘float32’)
    x_train    /= 255
    x_test     /= 255

 # convert class vectors to binary class matrices
 y_train = tf.keras.utils.to_categorical(y_train, NUM_CLASSES)
 y_test = tf.keras.utils.to_categorical(y_test, NUM_CLASSES)

 # train dataset
 train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))
 train_ds = train_ds.repeat()
 train_ds = train_ds.map(lambda x, y: (tf.cast(x, cast_dtype), y))
 train_ds = train_ds.batch(64, drop_remainder=True)

 # eval dataset
 eval_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
 eval_ds = eval_ds.repeat()
 eval_ds = eval_ds.map(lambda x, y: (tf.cast(x, cast_dtype), y))
 eval_ds = eval_ds.batch(64, drop_remainder=True)
 return train_ds, eval_ds, input_shape

Vamos agora criar uma função que construa o nosso modelo com vários parâmetros.

    def get_model(input_shape, dropout2_rate=0.5):
    
        # input image dimensions
        img_rows, img_cols = 28, 28

        # Define a CNN model to recognize MNIST.
        model = Sequential()
        model.add(Conv2D(32, kernel_size=(3, 3), activation='relu'   input_shape=input_shape, name='conv2d_1'))
        model.add(Conv2D(64, (3, 3), activation='relu', name='conv2d_2'))
        model.add(MaxPooling2D(pool_size=(2, 2), name='maxpool2d_1'))
        model.add(Dropout(0.25, name='dropout_1'))
        model.add(Flatten(name='flatten'))
        model.add(Dense(128, activation='relu', name='dense_1'))
        model.add(Dropout(dropout2_rate, name='dropout_2'))
        model.add(Dense(NUM_CLASSES, activation='softmax', name='dense_2'))
    
    return model

Vamos definir uma função parcial recebe três argumentos — input_shape, verbose e fit_with, que possuem valores fixos durante o tempo de execução. Você pode criar funções parciais no python usando a função parcial da biblioteca functools.

Funções parciais permitem derivar uma função com parâmetros x para uma função mais limitada, com menos parâmetros e valores fixos definidos .

    from functools import partial

    input_shape      = input_shape
    verbose          = 1
    fit_with_partial = partial(fit_with, input_shape, verbose)

A seguir definiremos a função que treinará o nosso modelo buscando os melhores hiperparâmetros e será passada ao otimizador bayesiano.

A função otimizará dois hiperparâmetros, a taxa de dropout da camada dropout_2 e o valor da taxa de aprendizado, treinando o modelo por 5 épocas e gerando a precisão da avaliação para o otimizador bayesiano.

    def fit_with(input_shape, verbose, dropout2_rate, lr):

    # Create the model using a specified hyperparameters.
    model = get_model(input_shape, dropout2_rate)

    # Train the model for a specified number of epochs.
    optimizer= Adam(lr = lr)
    
    model.compile(optimizer=optimizer, 
    loss = 'mse', 
    metrics = ['accuracy'])

    # Train the model with the train dataset.
    model.fit(train_ds,
    validation_data  = eval_ds,
    epochs           = 5,
    validation_steps = 60000 // 32, 
    steps_per_epoch  = 60000 // 32, 
    verbose = verbose)
    # Evaluate the model with the eval dataset.
    score = model.evaluate(eval_ds, steps = 10, verbose=1)
    
    print('Test loss:', score[0])
    print('Test accuracy:', score[1])
    print('\n')
    # Return the accuracy.
    return score[1]

O otimizador bayesiando é definido a seguir, sem a necessidade de configurações complexas. A idéia é simples, o construtor recebe a função a ser otimizada, bem como os intervalos dos hiperparâmetros a serem buscados. O objetivo principal é maximizar a precisão da avaliação, considerando os hiperparâmetros.

    from bayes_opt import BayesianOptimization

    bounds = {'dropout2_rate': (0.1, 0.5), 
              'lr'           : (1e-4, 1e-2)}

    optimizer = BayesianOptimization(f = fit_with_partial,
                                     pbounds      = bounds_2,
                                     verbose      = 1, # verbose = 1 prints only when a maximum is observed,
                                     verbose      = 0  # is silent
                                     random_state = 1)

    optimizer.maximize(init_points = 10, n_iter = 2)

    for i, res in enumerate(optimizer.res):
        print("Iteration {}: \n\t{}".format(i, res))
        print(optimizer.max)

Na definição do otimizador existem muitos parâmetros que podem ser passados, dentre os quais dois merecem destaque:

• n_iter: Quantas etapas da otimização bayesiana você deseja executar. Quanto mais etapas, maior a probabilidade de você encontrar um bom valor máximo.
• init_points: Quantas etapas de exploração aleatória você deseja executar. A exploração aleatória pode ajudar diversificando o espaço de exploração. Depois de 12 iterações, a construção do modelo com os hiperparâmetros encontrados atinge uma precisão de avaliação de 99,3%.

Lembrando que esses resultados não devem ser considerados para um modelo em produção, eles são apenas considerados para um ambiente isolado que é nosso experimento.

Epoch 4/5
1875/1875 [==============================] - 446s 238ms/step - loss: 0.0019 - acc: 0.9881 - val_loss: 0.0018 - val_acc: 0.9882
Epoch 5/5
1875/1875 [==============================] - 448s 239ms/step - loss: 0.0016 - acc: 0.9896 - val_loss: 0.0016 - val_acc: 0.9896
10/10 [==============================] - 0s 44ms/step - loss: 0.0013 - acc: 0.9937
Test loss: 0.0013259890803965391
Test accuracy: 0.99375


|  12       |  0.9937   |  0.3883   |  0.000207 |
=================================================

É possível ainda imprimir os melhores parametros atavés da seguinte chamada:

print(optimizer.max)
{'target': 0.9937499761581421, 
 'params': {'dropout2_rate': 0.3883228578249672, 
                       'lr': 0.00020765186492235896}}

Posteriormente basta voltarmos a nossa rede neural e adicionar tais hiperparâmetros validando o resultado e verificando se alcançamos a precisão esperada. No entando alguns pontos aqui merecem destaque:

• Conjunto de Dados: Aqui para fins didáticos utilizamos o mnist, mas fique a vontade para utilizar o seu próprio conjunto de dados o que faz muito mais sentido, dado que o mnist é um conjunto de dados amplamente utilizado e já vem normalizado de fábrica, o que não acontece com problemas reais.

• Hiperparâmetros: Novamente para fins didáticos, otimizamos apenas a camada dropout e a taxa de aprendizado, mas é possível utilizar a otimização bayesiana para otimizar também filtros, kernels inclusive quais camadas vão compor o nosso modelo, bastando apenas adaptar a aquitetura.

• Validação: Para esse artigo utilizamos a precisão, que não é a melhor das métricas a ser avaliada, mas foi útil para exemplificar o processo de otmização. O ideal é utilizar mais de uma métrica, bem como identificar se a métrica a ser utilizada realmente faz sentido ao problema que você deseja resolver.

Conclusão

A idéia geral desse artigo foi esclarecer um pouco como efetuar uma busca efetiva por hiperparâmetros aplicando otimização bayesiana em redes neurais convolucionais, uma técnica que é comprovada cientificamente ser mais eficiente que outros métodos como o Grid Search. Além disso, apresentamos a definição de processos gaussianos e qual o papel desses processos na otimização.

Finalmente, espero que esse material tenha sido útil e faça sentido pra você, principalmente aos iniciantes. Além disso nas referências do artigo é possível encontrar um material muito útil utilizado para elaboração desse artigo que pode te ajudar a ampliar seus conhecimentos no tema.

Lembrando que qualquer feedback, seja positivo ou negativo é so entrar em contato através do meu twitter, LinkedIn, Github ou nos comentário aqui em baixo. Obrigado :)