Uma introdução aos diferentes tipos de convoluções

Disclaimer: Neste artigo abordaremos apenas as convoluções 2D.

As redes neurais convolucionais profundas (CNNs) estão no centro de avanços espetaculares em aprendizado profundo. Embora as CNNs tenham sido usadas desde os anos 90 para resolver tarefas de reconhecimento de caracteres (Le Cun et al., 1997), sua ampla aplicação atual se deve a trabalhos muito mais recentes, quando uma CNN profunda foi usada para superar o estado da arte no desafio de classificação de imagens ImageNet (Krizhevsky et al., 2012).

As redes neurais convolucionais, portanto, constituem uma ferramenta muito útil para os praticantes de aprendizado de máquina. No entanto, aprender a usar CNNs pela primeira vez geralmente é uma experiência intimidadora. A forma de saída de uma camada convolucional é afetada pela forma de sua entrada, bem como pela escolha do kernel, preenchimento com zeros(padding) e passos, e o relacionamento entre essas propriedades não é trivial inferir. Isso contrasta com as camadas totalmente conectadas, cujo tamanho de saída é independente do tamanho de entrada. Além disso, as CNNs também apresentam um estágio denominado pooling, adicionando mais um nível de complexidade em relação às redes totalmente conectadas.

Finalmente, as chamadas camadas convolucionais transpostas (também conhecidas como camadas convolucionais fracionadas) têm sido empregadas em cada vez mais trabalhos ultimamente (Zeiler et al., 2011; Zeiler e Fergus, 2014; Long et al., 2015; Radford et al., 2015; Visin et al., 2015; Im et al., 2016), e sua relação com as camadas convolucionais foi explicada com vários graus de clareza.

Operação de Convolução

Antes de apresentarmos os tipos de convoluções, é muito importante entender as diferentes operações que normalmente são usadas em uma Rede Convolucional.

Existem duas entradas para uma operação convolucional

i) Uma imagem de entrada de tamanho \(3 \times 3 \times 3\)(\(Altura \times Largura \times Canais\))

ii) Um conjunto de filtros ‘k’ (também chamados de kernels ou extratores de características) cada um de tamanho (\(f \times f \times Canais\)), onde \(f\) é tipicamente 3 ou 5.

A saída de uma operação convolucional também é uma imagem 3D (também chamada de imagem de saída ou mapa de características) de tamanho (\(n_{out} \times n_{out} \times k\)).

A relação entre \(n_{in} e\)n_{out}$$ é a seguinte:

\begin{align} n_{out} = \left[ \frac{n_{in} + 2_p - k}{s} \right] +1 \end{align}

• \(n_{in}\): Número de características de entrada.

• \(n_{out}\): Número de características de saída.

• \(k\): Tamanho do kernel de convolução.

• \(p\): Tamanho do padding de convolução.

• \(p\): Tamanho do stride de convolução.

Logo, a operação de convolução pode ser visualizada abaixo:

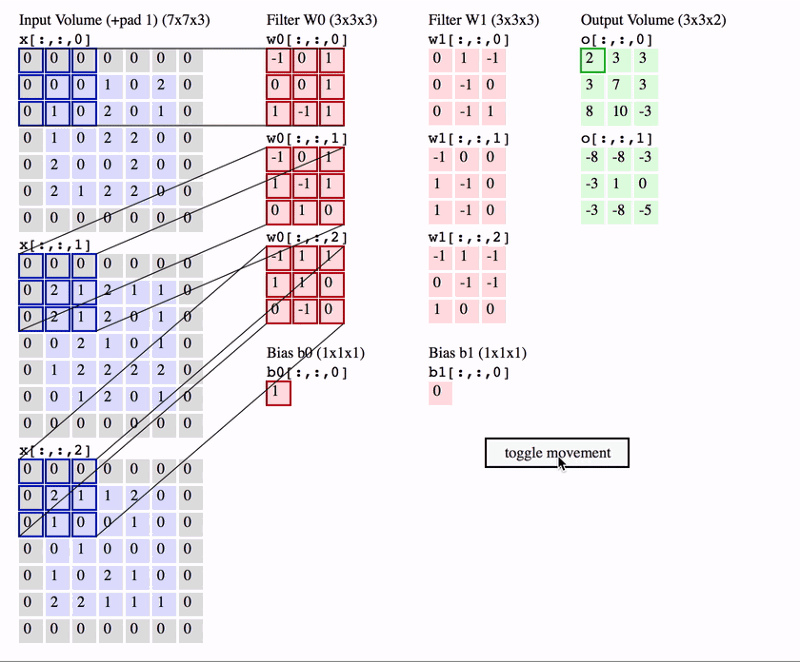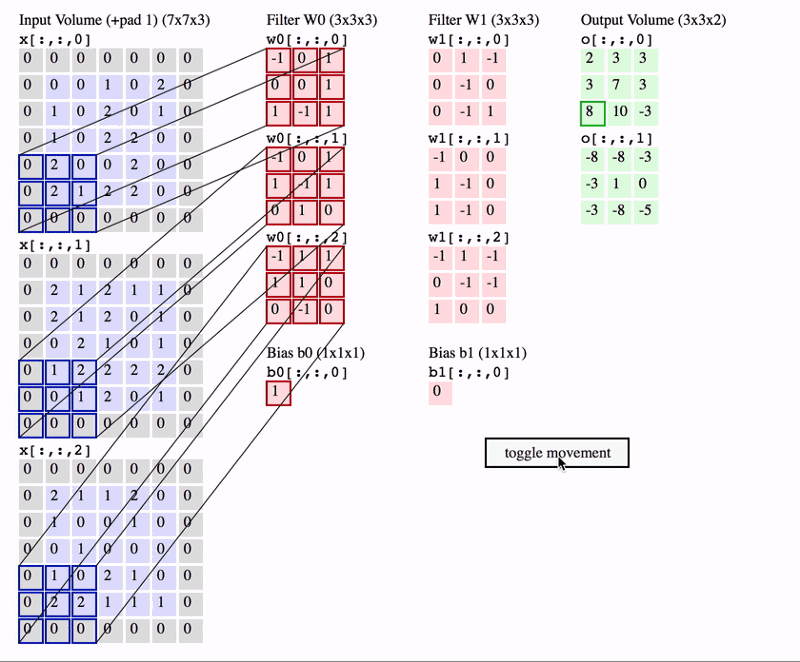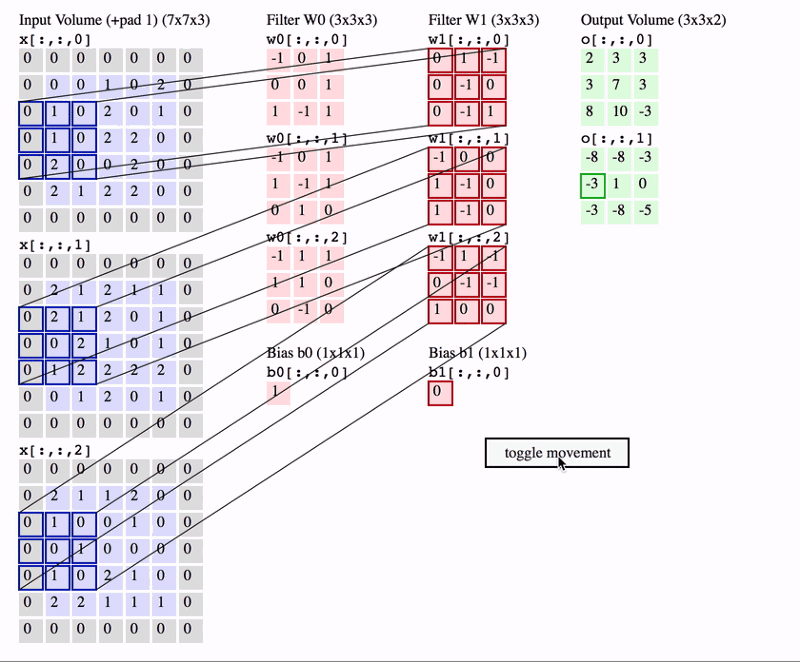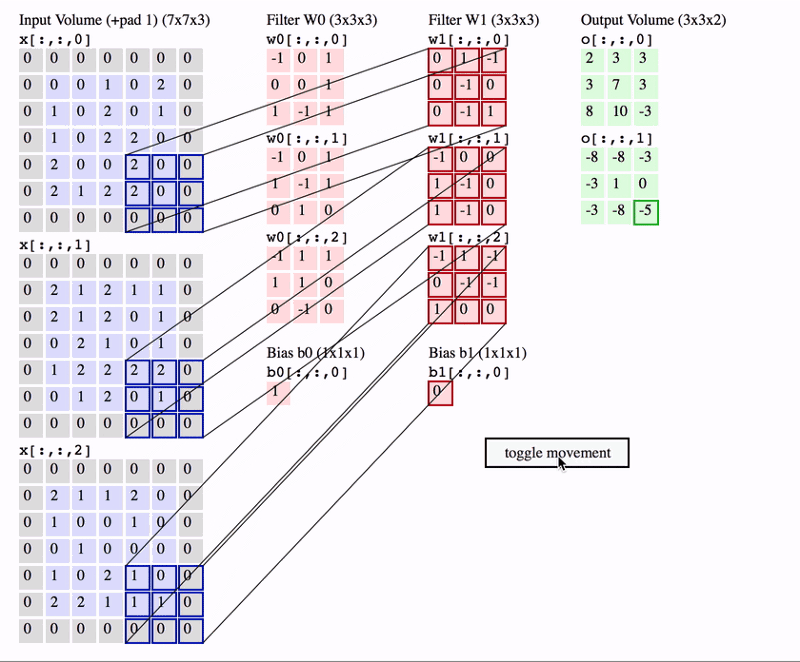
Na animação acima, temos um volume de entrada de tamanho \(7 \times 7 \times 3\). Dois filtros cada um de tamanho \(3 \times 3 \times 3\). Padding=0 e Stride=2. Portanto, o volume de saída é \(3 \times 3 \times 2\).

Se você não estiver confortável com essa aritmética, talvez seja necessários revisar os conceitos de Redes Convolucionais antes de continuar.

Convolução Discreta

Convolução é o nome dado a uma operação matemática entre dois sinais, cuja saída é um terceiro sinal. Um vetor é recebido como entrada e multiplicado por uma matriz para produzir uma saída (à qual um vetor de polarização é geralmente adicionado antes de passar o resultado por uma não linearidade). Isso é aplicável a qualquer categoria de entrada, seja uma imagem, um clipe de som ou uma coleção desordenada de recursos: qualquer que seja sua dimensionalidade, sua representação sempre pode ser achatada em um vetor antes da transformação. Imagens, clipes de som e muitos outros tipos semelhantes de dados têm uma estrutura intrínseca. Mais formalmente, eles compartilham essas propriedades importantes:

• Eles são armazenados como arrays multidimensionais.
• Eles apresentam um ou mais eixos para os quais a ordenação é importante — por exemplo, eixos de largura e altura para uma imagem, eixo de tempo para um clipe de som.
• Um eixo, chamado eixo do canal, é usado para acessar diferentes visualizações dos dados — por exemplo, os canais vermelho, verde e azul de uma imagem colorida ou os canais esquerdo e direito de uma faixa de áudio estéreo.

Essas propriedades não são exploradas quando uma transformação afim é aplicada; de fato, todos os eixos são tratados da mesma forma e a informação topológica não é considerada. Ainda assim, aproveitar a estrutura implícita dos dados pode ser muito útil na resolução de algumas tarefas, como visão computacional e reconhecimento de fala, e nesses casos seria melhor preservá-la. É aqui que as circunvoluções discretas entram em jogo.

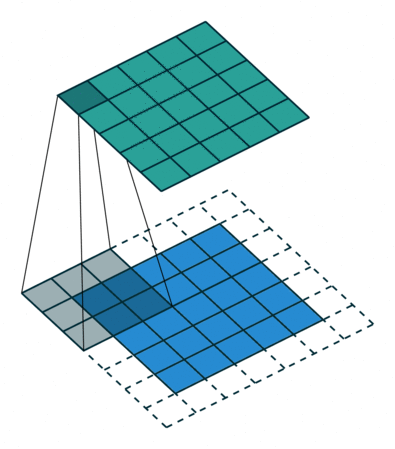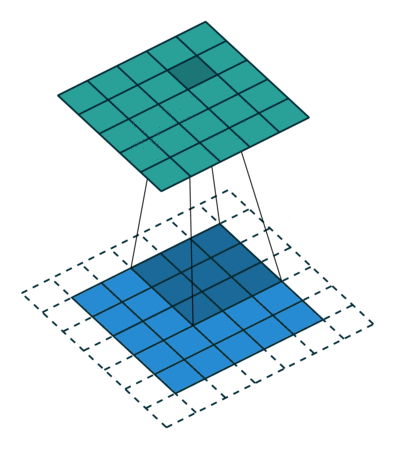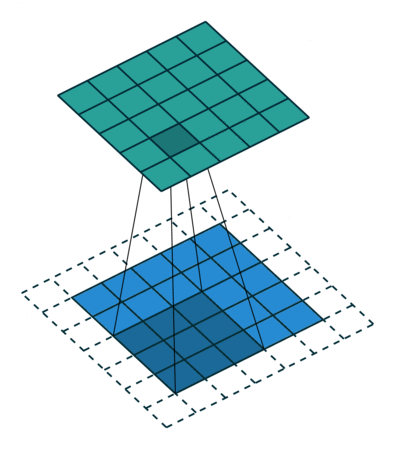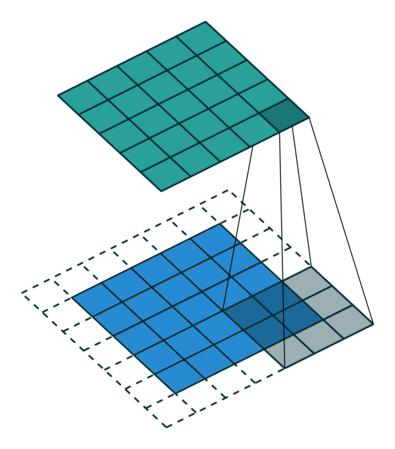
Uma convolução discreta é uma transformação linear que preserva a noção de ordenação. É esparso (apenas algumas unidades de entrada contribuem para uma determinada unidade de saída) e reutiliza parâmetros (os mesmos pesos são aplicados a vários locais na entrada).

A Figura 1 anterior fornece um exemplo de uma convolução discreta. A grade azul clara é chamada mapa de recursos de entrada. Para manter o desenho simples, um único mapa de recursos de entrada é representado, mas não é incomum ter vários mapas de recursos empilhados um sobre o outro.

A cada passo, o produto entre cada elemento do kernel e o elemento de entrada que ele sobrepõe é calculado e os resultados são somados para obter a saída no local atual. O procedimento pode ser repetido usando kernels diferentes para formar quantos mapas de recursos de saída forem desejados. As saídas finais deste procedimento são chamadas mapas de recursos de saída. Se houver vários mapas de recursos de entrada, o kernel terá que ser tridimensional — ou, equivalentemente, cada um dos mapas de recursos sofrerá uma operação de convolução com um kernel distinto — e os mapas de recursos resultantes serão somados elemento a elemento para produzir o mapa de recursos de saída. A convolução representada na Figura 1 é uma instância de uma convolução 2-D, mas pode ser generalizada para convoluções N-D.

Por exemplo, em uma convolução 3-D, o kernel seria um cuboide e deslizaria pela altura, largura e profundidade do mapa de recursos de entrada.

Convolução Transposta

Convoluções transpostas — também chamadas convoluções fracionadas ou deconvoluções — funcionam trocando as passagens para frente e para trás de uma convolução. Uma maneira de colocar isso é observar que o kernel define uma convolução, mas se é uma convolução direta ou uma convolução transposta é determinado por como os passos para frente e para trás são calculados. Assim, O objetivo de uma Convolução Transposta é fazer o oposto de uma Convolução regular, ou seja, aumentar a amostragem do mapa de recursos de entrada para um mapa de recursos de saída de tamanho maior desejado.

Algumas fontes usam o nome deconvolução, o que é inadequado porque não é uma deconvolução. No entando, as deconvoluções existem, mas não são comuns no campo do aprendizado profundo.

Uma deconvolução em verdade reverte o processo de uma convolução. Imagine inserir uma imagem em uma única camada convolucional. Agora pegue a saída, jogue-a em uma caixa preta e sairá sua imagem original novamente. Esta caixa preta faz uma deconvolução. É o inverso matemático do que uma camada convolucional faz.

A necessidade de convoluções transpostas geralmente surge do desejo de usar uma transformação indo na direção oposta de uma convolução normal, ou seja, de algo que tenha a forma de saída de alguma convolução para algo que tenha a forma de sua entrada mantendo uma padrão de conectividade compatível com a referida convolução.

Por exemplo, pode-se usar uma transformação como a camada de decodificação de um autoencoder convolucional ou projetar mapas de recursos para um espaço de dimensão superior.

Uma convolução transposta é um pouco semelhante porque produz a mesma resolução espacial que uma hipotética camada deconvolucional produziria. No entanto, a operação matemática real que está sendo executada nos valores é diferente. Uma camada convolucional transposta realiza uma convolução regular, mas reverte sua transformação espacial.

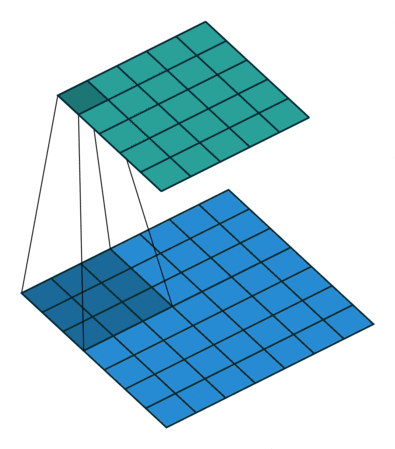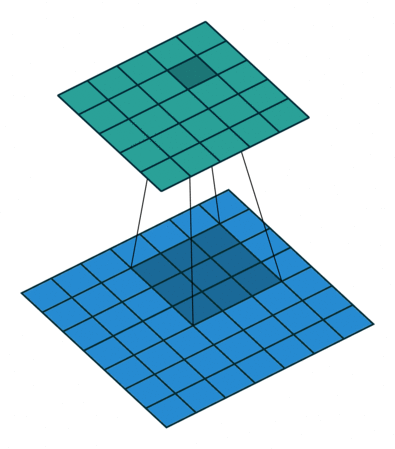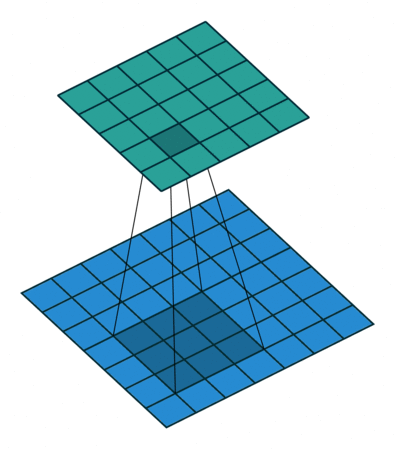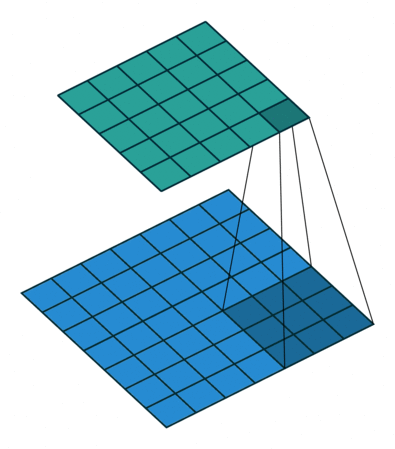
Neste ponto, você deve estar bastante confuso, então vamos ver um exemplo concreto. Uma imagem de \(5 \times 5\) é alimentada em uma camada convolucional. O passo é definido como 2, o preenchimento é desativado e o kernel é \(3 \times 3\). Isso resulta em uma imagem \(2 \times 2\).

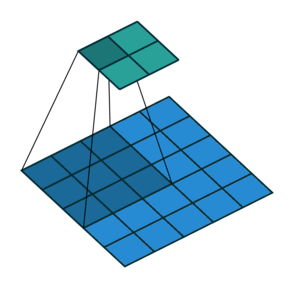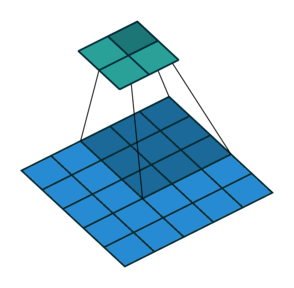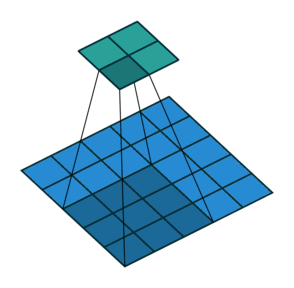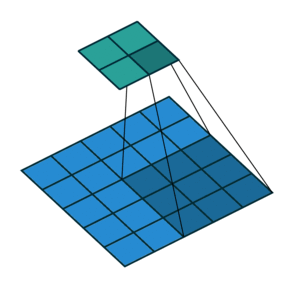
Se quiséssemos reverter esse processo, precisaríamos da operação matemática inversa para que 9 valores sejam gerados a partir de cada pixel inserido. Depois, percorremos a imagem de saída com um passo de 2. Isso seria uma deconvolução.

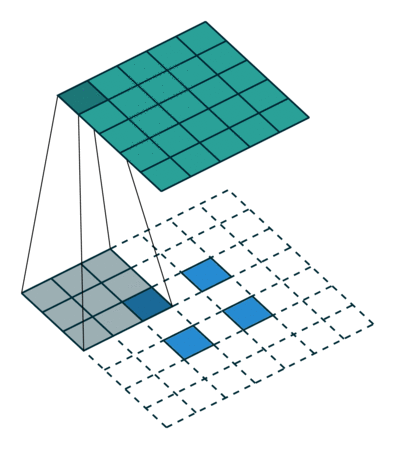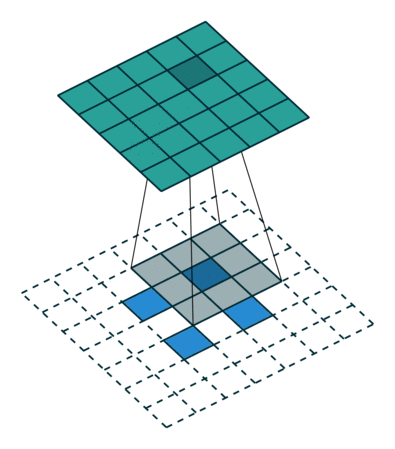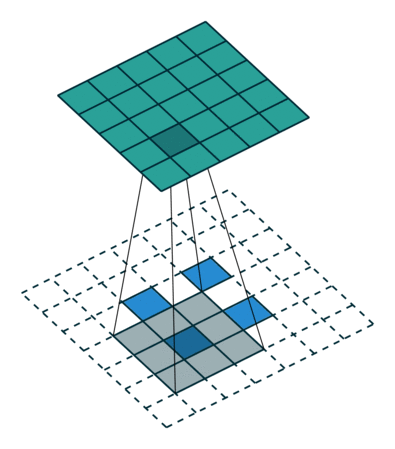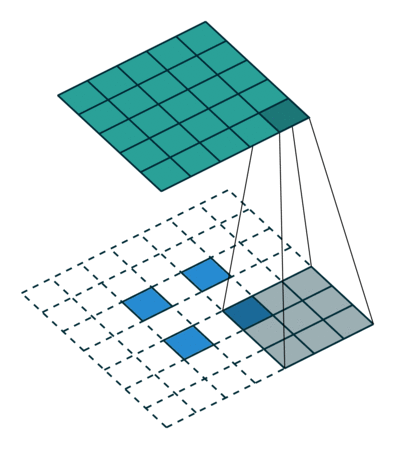
Para que servem as Convoluções Transpostas?

Convoluções Transpostas são cruciais para a segmentação semântica e geração de dados nas Redes Adversariais Generativas (GANs). Um dos exemplos mais diretos seria uma Rede Neural treinada para aumentar a resolução da imagem.

Convolução Transposta vs. Deconvolução

Deconvolução é um termo que flutua ao lado de convoluções transpostas, e os dois são frequentemente confundidos. Muitas fontes usam os dois de forma intercambiável e, embora existam deconvoluções, elas não são muito populares no campo de aprendizado de máquina.

Uma deconvolução é uma operação matemática que reverte o efeito da convolução. Imagine lançar uma entrada através de uma camada convolucional e coletar a saída. Agora jogue a saída pela camada deconvolucional e você receberá a mesma entrada. É o inverso da função convolucional multivariada.

Por outro lado, uma camada convolucional transposta apenas reconstrói as dimensões espaciais da entrada. Em teoria, isso é bom para o aprendizado profundo, pois a rede pode aprender seus próprios parâmetros por meio do gradiente descendente, no entanto, a rede não fornece a mesma saída que a entrada. Logo, A operação de convolução transposta pode ser pensada como o gradiente de alguma convolução em relação à sua entrada, que geralmente é como as convoluções transpostas são implementadas na prática.

Convolução Dilatada

Leitores familiarizados com a literatura de aprendizado profundo podem ter notado que o termo “convoluções dilatadas” (ou “convoluções atrous”, da expressão francesa convolutions à trous) aparece em artigos recentes. Aqui tentamos fornecer uma compreensão intuitiva das convoluções dilatadas e para uma descrição mais aprofundada e para entender em que contextos eles são aplicados, ver Chen et al. (2014); Yu e Koltun (2015).

Convoluções dilatadas “inflam” o kernel inserindo espaços entre os elementos do kernel introduzindo outro parâmetro para camadas convolucionais chamado taxa de dilatação. A “taxa” de dilatação é controlada por um hiperparâmetro adicional.

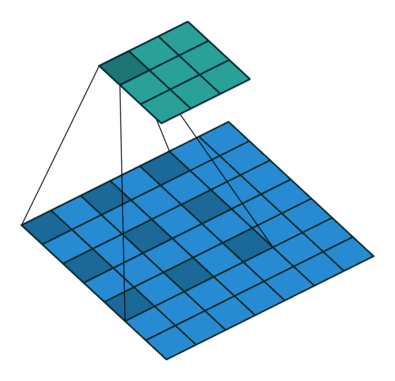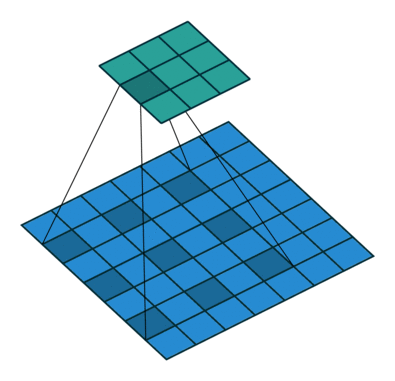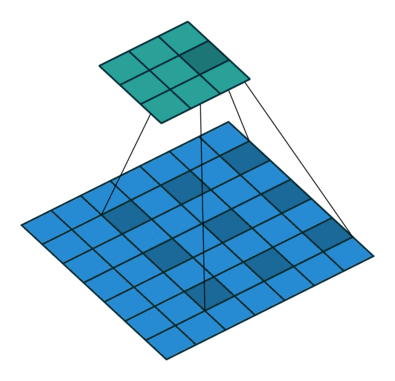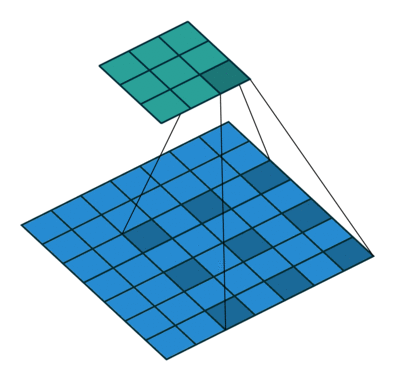
As convoluções dilatadas são usadas para aumentar de forma pouco custosa o campo receptivo das unidades de saída sem aumentar o tamanho do kernel, o que é especialmente eficaz quando várias convoluções dilatadas são empilhadas uma após a outra.

Um exemplo de aplicação pode ser visto em Oord et al. (2016), onde o modelo WaveNet proposto implementa um modelo generativo autorregressivo para áudio bruto que usa convoluções dilatadas para condicionar novos quadros de áudio em um contexto de quadros de áudio anteriores.

Logo, as convoluções dilatadas oferecem um campo de visão mais amplo com o mesmo custo computacional. Convoluções dilatadas são particularmente populares no campo da segmentação em tempo real. Use-os se precisar de um amplo campo de visão e não puder pagar várias convoluções ou kernels maiores.

Convoluções Separáveis

Em uma convolução separável, podemos dividir a operação do kernel em várias etapas. Vamos expressar uma convolução como \(y = conv(x, k)\) onde \(y\) é a imagem de saída, \(x\) é a imagem de entrada e \(k\) é o kernel. Em seguida, vamos supor que k pode ser calculado por: \(k = k1.dot(k2)\). Isso a tornaria uma convolução separável porque em vez de fazer uma convolução 2D com k, poderíamos obter o mesmo resultado fazendo 2 convoluções 1D com k1 e k2.

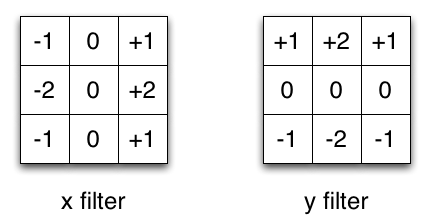
Por exemplo, o kernel Sobel, que é frequentemente usado no processamento de imagens. Você pode obter o mesmo kernel multiplicando o vetor \([1, 0, -1]\) e \([1,2,1].T\). Isso exigiria 6 em vez de 9 parâmetros ao fazer a mesma operação. O exemplo acima mostra o que é chamado de convolução espacial separável, que, até onde sei, não é usada em aprendizado profundo.

Desse modo, pode-se criar algo muito semelhante a uma convolução separável espacial empilhando uma camada de kernel \(1 \times N\) e \(N \times 1\). Isso foi usado recentemente em uma arquitetura chamada EffNet mostrando resultados promissores Freeman et al., 2018.

No campo do aprendizado profundo, geralmente usamos algo chamado convolução separável profunda. Isso executará uma convolução espacial, mantendo os canais separados e, em seguida, seguirá com uma convolução em profundidade.

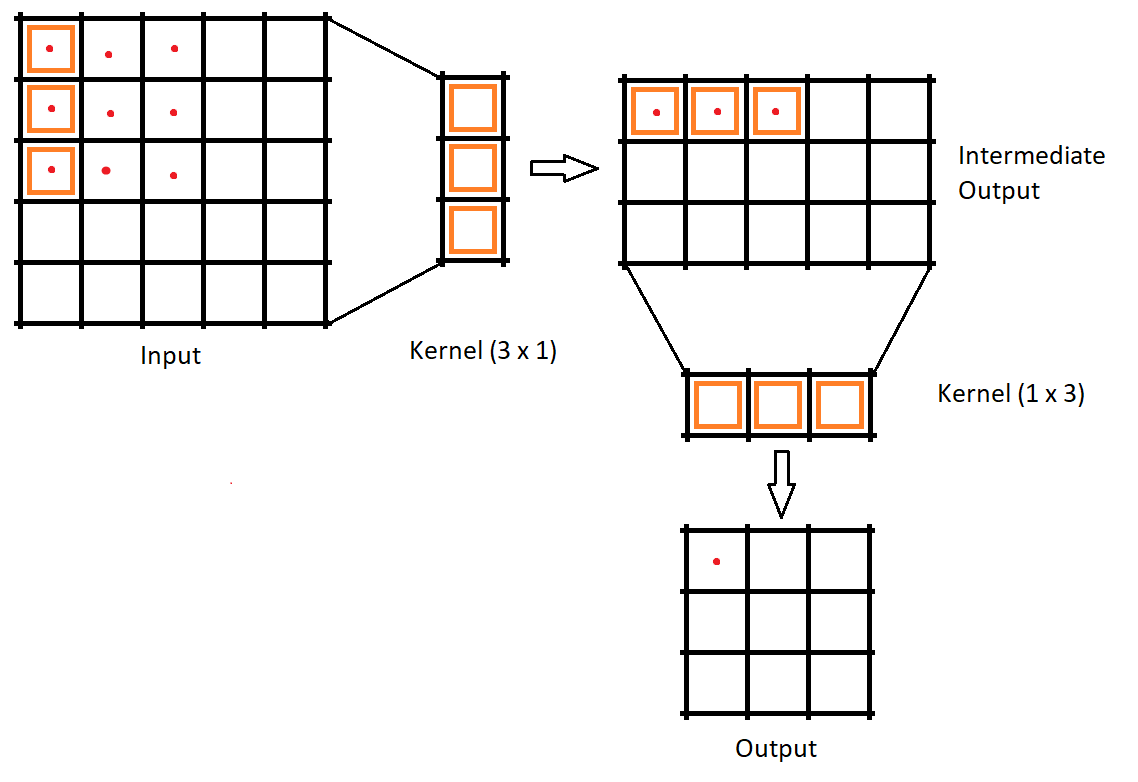
Nas convoluções convencionais, se o kernel é \(3 \times 3\) então o número de parâmetros seria 9. Na convolução espacialmente separável dividimos o kernel em dois kernels de formas \(3 \times 1\) e \(1 \times 3\). A entrada é primeiro convolucionada com \(3 \times 1\) kernel e então com \(1 \times 3\), então o número de parâmetros seria 3 + 3 = 6. Portanto, uma menor operação de multiplicação de matrizes é necessária. Uma coisa importante a notar aqui é que nem todo kernel pode ser separado. Devido a essa desvantagem, esse método é menos usado em comparação com as convoluções separáveis em profundidade.

Convoluções separáveis são ótimas quando você está otimizando o modelo para tamanho menor ou velocidade mais alta, comprometendo menos a precisão. Não é aconselhável usá-lo quando você estiver otimizando o modelo para precisão. Muitos algoritmos de aprendizado profundo são construídos usando convoluções separáveis, um deles é o algoritmo Xception, Convoluções separáveis ​​em profundidade também são usadas para dispositivos móveis devido ao uso eficiente de parâmetros.

Resumo

• Uma camada convolucional extrai recursos da camada e reduz a amostragem da entrada.
• Técnicas como a dilatação, bem como upsampling e downsampling e padding, controlam o tamanho da saída.
• Uma camada convolucional transposta tenta reconstruir as dimensões espaciais da camada convolucional e reverte as técnicas de downsampling e upsampling aplicadas a ela.
• Uma deconvolução é apenas uma operação matemática que reverte o processo de uma camada convolucional.

Considerações Finais

Se você leu esse post até aqui, muito obrigado, espero que esse material tenha sido útil e faça sentido para você. É valido mencionar que ao longo do artigo muitos links foram disponibilizados e possuem um conteúdo extremante rico, além disso, na seção de referências é possível encontrar mais alguns links uteis que foram utilizados para elaboração desse artigo que pode te ajudar a ampliar seus conhecimentos no tema assim como me ajudaram.

Finalmente caso algum outro assunto relacionado ou não com o conteúdo desse post te interesse, ou tenha te deixado em dúvida, coloca aí nos comentários que ficarei muito feliz de trazer o conteúdo de forma mais clara em um novo post.

Lembrando que qualquer feedback, seja positivo ou negativo é basta entrar em contato através do meu twiter, linkedin, Github ou nos comentários aqui em baixo. Obrigado :)